题目内容
16.先化简:$\frac{{x}^{2}+x}{{x}^{2}-2x+1}$÷($\frac{2}{x-1}$-$\frac{1}{x}$),再从-2<x<3的范围内选取一个你喜欢的x值代入求值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,确定出x的值,代入计算即可求出值.
解答 解:原式=$\frac{x(x+1)}{(x-1)^{2}}$÷$\frac{2x-x+1}{x(x-1)}$=$\frac{x(x+1)}{(x-1)^{2}}$•$\frac{x(x-1)}{x+1}$=$\frac{{x}^{2}}{x-1}$,
当x=2时,原式=4(x≠-1,0,1).
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
6.在?ABCD中,∠A=55°,则∠C的大小为( )
| A. | 135° | B. | 125° | C. | 115° | D. | 55° |
7. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
 如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )| A. | 50° | B. | 60° | C. | 40° | D. | 30° |
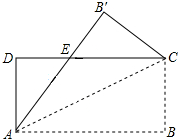 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.试找出一个与△AED全等的三角形,并加以证明.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.试找出一个与△AED全等的三角形,并加以证明. 如图,在平行四边形ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,平行四边形ABCD的周长是14,则DM等于3.
如图,在平行四边形ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,平行四边形ABCD的周长是14,则DM等于3. 如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )
如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )



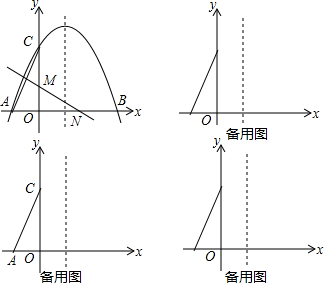 如图,抛物线y=ax2+bx+4经过点A(-2,0),B(6,0),与y轴交于C.
如图,抛物线y=ax2+bx+4经过点A(-2,0),B(6,0),与y轴交于C.