题目内容
15.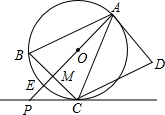 如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.
如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.(1)求证:∠BAP=∠CAP;
(2)判断直线PC与⊙O的位置关系,并说明理由;
(3)若AB=9,BC=6,求PC的长.
分析 (1)由AD是⊙O的切线,BC∥AD,易得AO⊥BC,然后由垂径定理求得$\widehat{BE}$=$\widehat{CE}$,继而证得结论;
(2)过C点作直径CF,连接FB,由CF为直径得∠F+∠BCE=90°,由AB∥DC得∠ACD=∠BAC,而∠BAC=∠F,∠BCP=∠ACD,所以∠F=∠BCP,于是∠BCP+∠BCF=90°,然后根据切线的判断得到结论;
(3)根据切线的性质得到OA⊥AD,而BC∥AD,则AM⊥BC,根据垂径定理求得BM与CM的长,根据等腰三角形性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM=6$\sqrt{2}$,设⊙O的半径为r,则OC=r,OM=AM-r=6$\sqrt{2}$-r,在Rt△OCM中,根据勾股定理计算出r的值即可.
解答 (1)证明:∵AD是⊙O的切线,
∴OA⊥AD,
∵BC∥AD,
∴OA⊥BC,
∴$\widehat{BE}$=$\widehat{CE}$,
∴∠BAP=∠CAP;
(2)PC与圆O相切,理由为:
解:过C点作直径CF,连接EB,如图,
∵CE为直径,
∴∠FBC=90°,即∠F+∠BCF=90°,
∵AB∥DC,
∴∠ACD=∠BAC,
∵∠BAC=∠F,∠BCP=∠ACD.
∴∠F=∠BCP,
∴∠BCP+∠BCF=90°,即∠PCF=90°,
∴CF⊥PC,
∴PC与圆O相切;
(3)解:∵AD是⊙O的切线,切点为A
∴OA⊥AD,
∵BC∥AD,
∴AM⊥BC,
∴BM=CM=$\frac{1}{2}$BC=3,
∴AC=AB=9,
在Rt△AMC中,AM=$\sqrt{A{C}^{2}-C{M}^{2}}$=6$\sqrt{2}$,
设⊙O的半径为r,则OC=r,OM=AM-r=6$\sqrt{2}$-r,
在Rt△OCM中,OM2+CM2=OC2,即32+(6$\sqrt{2}$-r)2=r2,
解得:r=$\frac{27\sqrt{2}}{8}$,
∴CF=2r=$\frac{27\sqrt{2}}{4}$,OM=6$\sqrt{2}$-$\frac{27\sqrt{2}}{8}$=$\frac{21\sqrt{2}}{8}$,
∴BF=2OM=$\frac{21\sqrt{2}}{4}$,
∵∠F=∠MCP,
∴△PCM∽△CFB,
∴PC:CF=CM:FB,
∴$\frac{PC}{\frac{27\sqrt{2}}{4}}$=$\frac{3}{\frac{21\sqrt{2}}{4}}$,
∴PC=$\frac{27}{7}$.
点评 此题属于圆的综合题,考查了切线的性质、垂径定理、圆周角定理以及勾股定理等知识.注意准确作出辅助线、利用方程思想求解是解此题的关键.

 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFGC=$\sqrt{3}-1$中,说法正确的是( )
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFGC=$\sqrt{3}-1$中,说法正确的是( )| A. | ①③④ | B. | ②③ | C. | ①③ | D. | ①②③ |
| A. | 5≤S≤8 | B. | 5≤S≤9 | C. | 5≤S≤10 | D. | S≤5或S≥8 |
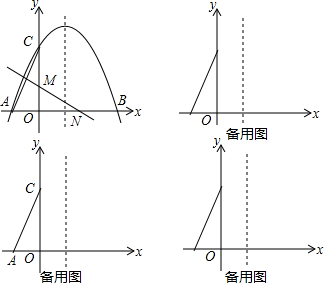 如图,抛物线y=ax2+bx+4经过点A(-2,0),B(6,0),与y轴交于C.
如图,抛物线y=ax2+bx+4经过点A(-2,0),B(6,0),与y轴交于C.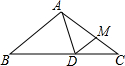 如图,在△ABC中,AB=AC=10,BC=16,D和M分别是BC、AC边上的动点,则AD+DM的最小值是$\frac{48}{5}$.
如图,在△ABC中,AB=AC=10,BC=16,D和M分别是BC、AC边上的动点,则AD+DM的最小值是$\frac{48}{5}$.