题目内容
17. 如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )
如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )| A. | $\frac{π}{2}$-1≤S<$\frac{4π}{3}$-$\sqrt{3}$ | B. | $\frac{π}{2}$-1≤S<$\frac{4π}{3}$-1 | C. | 1≤S<$\sqrt{3}$ | D. | $\sqrt{3}≤S$$<2\sqrt{3}$-1 |
分析 首先求出S关于r的函数表达式,分析其增减性;然后根据r的取值,求出S的最大值与最小值,从而得到S的取值范围.
解答  解:如右图所示,过点D作DG⊥BC于点G,易知G为BC的中点,CG=1.
解:如右图所示,过点D作DG⊥BC于点G,易知G为BC的中点,CG=1.
在Rt△CDG中,由勾股定理得:DG=$\sqrt{C{D}^{2}-C{G}^{2}}$=$\sqrt{{r}^{2}-1}$.
设∠DCG=θ,则由题意可得:
S=2(S扇形CDE-S△CDG)=2($\frac{θπ{r}^{2}}{360}$-$\frac{1}{2}$×1×$\sqrt{{r}^{2}-1}$)=$\frac{θπ{r}^{2}}{180}$-$\sqrt{{r}^{2}-1}$,
∴S=$\frac{θπ•{r}^{2}}{180}$-$\sqrt{{r}^{2}-1}$.
当r增大时,∠DCG=θ随之增大,故S随r的增大而增大.
当r=$\sqrt{2}$时,DG=$\sqrt{{r}^{2}-1}$=1,∵CG=1,故θ=45°,
∴S=$\frac{45π•(\sqrt{2})^{2}}{180}$-$\sqrt{(\sqrt{2})^{2}-1}$=$\frac{π}{2}$-1;
若r=2,则DG=$\sqrt{{r}^{2}-1}$=$\sqrt{3}$,∵CG=1,故θ=60°,
∴S=$\frac{60π×{2}^{2}}{180}$-$\sqrt{{2}^{2}-1}$=$\frac{4π}{3}$-$\sqrt{3}$.
∴S的取值范围是:$\frac{π}{2}$-1≤S<$\frac{4π}{3}$-$\sqrt{3}$.
故答案为:$\frac{π}{2}$-1≤S<$\frac{4π}{3}$-$\sqrt{3}$.
点评 本题考查扇形面积的计算、等边三角形的性质、勾股定理等重要知识点.解题关键是求出S的函数表达式,并分析其增减性.

 名校课堂系列答案
名校课堂系列答案 如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )
如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是( )| A. | 50° | B. | 60° | C. | 40° | D. | 30° |
 如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )
如图,△ABC中,AB=AC=10,BC=12,动点P从A点出发,按A→B的方向在AB上移动,动点Q从B点出发,按B→C的方向在BC上移动(当P点到达点B时,P点和Q点停止移动,且两点的移动速度相等),记PA=x,△BPQ的面积为y,则y关于x的函数图象大致是( )



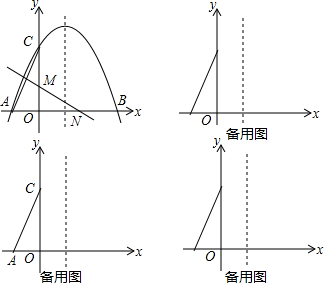 如图,抛物线y=ax2+bx+4经过点A(-2,0),B(6,0),与y轴交于C.
如图,抛物线y=ax2+bx+4经过点A(-2,0),B(6,0),与y轴交于C. 已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFGC=$\sqrt{3}-1$中,说法正确的是( )
已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论:①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFGC=$\sqrt{3}-1$中,说法正确的是( )