题目内容
1.(1)解方程:x2-2x-1=0;(2)解不等式组$\left\{\begin{array}{l}{x+2<4}\\{2(x-1)>-10}\end{array}\right.$.
分析 (1)利用公式法求出x的值即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)∵a=1,b=-2,c=-1,
∴△=b2-4ac=(-2)2-4×1×(-1)=8,
∴x=$\frac{2±2\sqrt{2}}{2}$,
∴x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$;
(2)$\left\{\begin{array}{l}x+2<4①\\ 2(x-1)>-10②\end{array}\right.$,
不等式①的解集为x<2,
不等式②的解集为x>-4,
则原不等式组的解集为-4<x<2.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平行四边形ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,平行四边形ABCD的周长是14,则DM等于3.
如图,在平行四边形ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,平行四边形ABCD的周长是14,则DM等于3.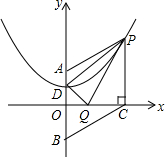 如图,抛物线y=$\frac{1}{4}$x2+bx+c的对称轴是y轴,点D,P在抛物线上,A(0,2),D(0,1),PC⊥x轴于点C,CB∥AP,交x轴于点B.
如图,抛物线y=$\frac{1}{4}$x2+bx+c的对称轴是y轴,点D,P在抛物线上,A(0,2),D(0,1),PC⊥x轴于点C,CB∥AP,交x轴于点B. 如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,FD=FG,BF=2$\sqrt{2}$,BG=3,则FH的长$\frac{2\sqrt{5}}{11}$.
如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,FD=FG,BF=2$\sqrt{2}$,BG=3,则FH的长$\frac{2\sqrt{5}}{11}$.