题目内容
4.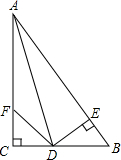 如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接
如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接DF.
(1)求证:AC=AE;
(2)若AC=8,AB=10,求DE的长;
(3)若CF=BE,直接写出线段AB,AF,EB的数量关系:AB=AF+2EB.
分析 (1)先过点D作DE⊥AB于E,由于DE⊥AB,那么∠AED=90°,则有∠ACB=∠AED,联合∠CAD=∠BAD,AD=AD,利用AAS可证.
(2)由△ACD≌△AED,证得DC=DE,然后根据S△ACB=S△ACD+S△ADB即可求得DE.
(3)由AC=AE,CF=BE,根据AB=AE+EB,AC=AF+CF即可证得.
解答 解:(1)∵∠C=90°,DE⊥AB,
∴∠C=∠AED=90°,
在△ACD和△AED中,
$\left\{\begin{array}{l}{∠CAD=∠BAD}\\{∠C=∠AED}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AED(AAS),
∴AC=AE.
(2)∵∠C=90°,AC=8,AB=10,
∴BC=6,
∴△ABC的面积等于24,
由(1)得:△ACD≌△AED,
∴DC=DE,
∵S△ACB=S△ACD+S△ADB,
∴S△ACB=$\frac{1}{2}$AC•CD+$\frac{1}{2}$AB•DE,
又∵AC=8,AB=10,
∴24=$\frac{1}{2}$×8×CD+$\frac{1}{2}$AB•DE
∴DE=$\frac{8}{3}$;
(3)∵AB=AE+EB,AC=AE,
∴AB=AC+EB,
∵AC=AF+CF,CF=BE
∴AB=AF+2EB.
故答案为:AB=AF+2EB.
点评 本题考查了直角三角形的性质、全等三角形的判定和性质,解题的关键是作辅助线,构造全等三角形.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
19.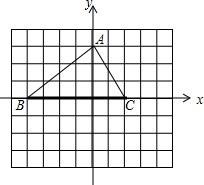 如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )
如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )
 如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )
如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )| A. | (-2,-3) | B. | (2,-3) | C. | (2,3) | D. | (0,3) |
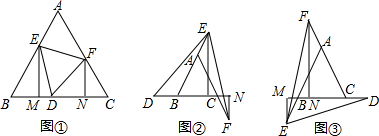
 如图,在△ABC中,AB=AC,AD⊥BC,E是AC的中点.若DE=5,则AB的长为10,若AD=8,则BC=12.
如图,在△ABC中,AB=AC,AD⊥BC,E是AC的中点.若DE=5,则AB的长为10,若AD=8,则BC=12.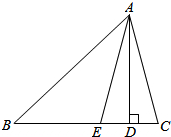 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.