题目内容
15．
如图，在△ABC中，AB=AC，AD⊥BC，E是AC的中点．若DE=5，则AB的长为10，若AD=8，则BC=12．
分析 根据等腰三角形的性质求出BD=DC，根据三角形的中位线得出AB=2DE，即可求出AB，根据勾股定理求出BD，即可求出BC．
解答 解：∵在△ABC中，AB=AC，AD⊥BC，
∴BD=DC，
∵E是AC的中点，DE=5，
∴AB=2DE=10，
∵在Rt△ADB中，由勾股定理得：BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∴BC=2BD=12，
故答案为：10，12．
点评 本题考查了三角形的中位线，等腰三角形的性质，勾股定理的应用，能求出AB的长是解此题的关键．
练习册系列答案
相关题目
6．
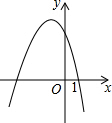二次函数y=ax2+bx+c的图象如图所示，则化简二次根式$\sqrt{（a+c）^{2}}$+$\sqrt{（b-c）^{2}}$的结果是（ ）
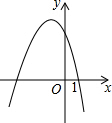二次函数y=ax2+bx+c的图象如图所示，则化简二次根式$\sqrt{（a+c）^{2}}$+$\sqrt{（b-c）^{2}}$的结果是（ ）| A． | a+b | B． | -a-b | C． | 2b-c | D． | -2b+c |
3．计算（2a3b）2的结果是（ ）
| A． | 2a3b2 | B． | 4a6b2 | C． | 2a6b2 | D． | 4a4b2 |
20．下列说法中错误的是（ ）
| A． | 任意三角形的内角和都是180° | |
| B． | 三角形按边分可分为不等边三角形和等腰三角形 | |
| C． | 三角形的中线、角平分线、高都是线段 | |
| D． | 三角形的一个外角大于任何一个内角 |
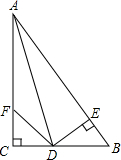如图，在△ABC中，∠C=90°，∠CAD=∠BAD，DE⊥AB于E，点F在边AC上，连接