题目内容
16.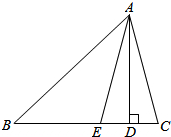 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
分析 由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=$\frac{1}{2}$∠BAC,故∠EAD=∠EAC-∠DAC.
解答 解:∵∠B=42°,∠C=70°,
∴∠BAC=180°-∠B-∠C=68°,
∵AE是角平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=34°.
∵AD是高,∠C=70°,
∴∠DAC=90°-∠C=20°,
∴∠EAD=∠EAC-∠DAC=34°-20°=14°,
∠AEC=90°-14°=76°.
点评 本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是熟练掌握三角形的内角和定理.

练习册系列答案
相关题目
6.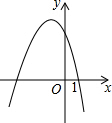 二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )
二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )
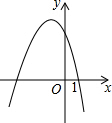 二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )
二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )| A. | a+b | B. | -a-b | C. | 2b-c | D. | -2b+c |
11.化简(a-1)•$\sqrt{\frac{1}{1-a}}$的结果是( )
| A. | -$\sqrt{1-a}$ | B. | $\sqrt{1-a}$ | C. | -$\sqrt{a-1}$ | D. | $\sqrt{a-1}$ |
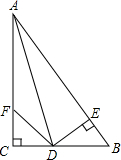 如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接
如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接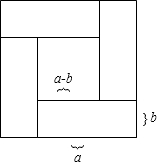 用四个相同的长方形与一个小正方形无重叠、无缝隙地拼成一个大正方形的图案(如图),则由图形能得出(a-b)2=(a+b)2-4ab(化为a、b两数和与积的形式)
用四个相同的长方形与一个小正方形无重叠、无缝隙地拼成一个大正方形的图案(如图),则由图形能得出(a-b)2=(a+b)2-4ab(化为a、b两数和与积的形式) 在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),把△AOB平移,使点A移至点D(2,1),点O、B的对应点分别是点E、F.
在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),把△AOB平移,使点A移至点D(2,1),点O、B的对应点分别是点E、F.