Question

15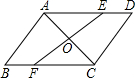．如图，AC是?ABCD的一条对角线，过AC中点O的直线分别交AD，BC于点E，F．
（1）求证：AE=CF；
（2）连接AF，CE．
①当EF和AC满足条件EF⊥AC时，四边形AFCE是菱形；
②若AB=1，BC=2，∠B=60°，则四边形AFCE为矩形时，EF的长是$\sqrt{3}$．

Answer 1

分析 （1）由平行四边形的性质可知OA=OC，∠AEO=∠OFC，∠EAO=∠OCF，证出△AOE≌△COF，即可得出AE=CF．
（2）①先证明四边形AFCE是平行四边形，由EF⊥AC，即可得出四边形AFCE是菱形；
②由矩形的性质得出EF=AC，∠AFB=∠AFC=90°，求出AF、CF，由勾股定理求出AC，即可得出EF的长．

解答 （1）证明：∵AD∥BC，
∴∠EAO=∠FCO．
∵O是AC的中点，
∴OA=OC，
在△AOE和△COF中，$\left\{\begin{array}{l}{∠EAO=∠FCO}&{\;}\\{OA=OC}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$，
∴△AOE≌△COF（ASA）．
∴AE=CF．
（2）解：①当EF和AC满足条件EF⊥AC时，四边形AFCE是菱形；理由如下：如图所示：
∵AE∥CF，AE=CF，
∴四边形AFCE是平行四边形，
又∵EF⊥AC，
∴四边形AFCE是菱形；
②若四边形AFCE为矩形，
则EF=AC，∠AFB=∠AFC=90°，
∵AB=1，BC=2，∠B=60°，
∴∠BAF=30°，
∴BF=$\frac{1}{2}$AB=$\frac{1}{2}$，
∴AF=$\sqrt{3}$BF=$\frac{\sqrt{3}}{2}$，CF=2-$\frac{1}{2}$=$\frac{3}{2}$，
∴AC=$\sqrt{A{F}^{2}+C{F}^{2}}$=$\sqrt{（\frac{\sqrt{3}}{2}）^{2}+（\frac{3}{2}）^{2}}$=$\sqrt{3}$，
∴EF=$\sqrt{3}$；
故答案为：$\sqrt{3}$．

点评 此题主要考查了全等三角形的性质与判定、平行四边形的性质与判定、菱形的判定、矩形的性质；熟练掌握菱形的判定和平行四边形的性质、矩形的性质是解决问题的关键．