题目内容
7. 如图所示,等腰直角三角形ABC与等腰直角三角形A′B′C′是位似图形,位似中心为点O,位似比1:2,点A的坐标为(1,0),点C的坐标为(0,1),则点B′的坐标为( )
如图所示,等腰直角三角形ABC与等腰直角三角形A′B′C′是位似图形,位似中心为点O,位似比1:2,点A的坐标为(1,0),点C的坐标为(0,1),则点B′的坐标为( )| A. | (2,2) | B. | (-2,2) | C. | (-2,-2) | D. | (2,2)或(-2,-2) |
分析 根据题意得出B点坐标,再利用位似图形的性质:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k,进而得出答案.
解答 解:由题意可得:B点坐标为:(1,1),
∵等腰直角三角形ABC与等腰直角三角形A′B′C′是位似图形,位似中心为点O,位似比1:2,
∴点B′的坐标为(2,2)或(-2,-2).
故选:D.
点评 此题主要考查了位似变换以及坐标与图形的性质,正确应用位似图形的性质是解题关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
18.期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是85分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是85分”,上面两位同学的话能反映出的统计量是( )
| A. | 众数和中位数 | B. | 众数和平均数 | C. | 平均数和中位数 | D. | 众数和方差 |
2.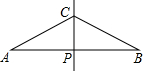 如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.
下列说法正确的是( )
 如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.
下列说法正确的是( )
| A. | 甲、乙都正确 | B. | 甲、乙都错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
12.-16的相反数是( )
| A. | -$\frac{1}{16}$ | B. | -16 | C. | $\frac{1}{16}$ | D. | 16 |
 如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: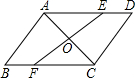 如图,AC是?ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
如图,AC是?ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.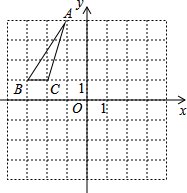 在如图所示的平面直角坐标系中,△ABC的三个顶点都在小正方形的顶点处,请结合图完成下列各题:
在如图所示的平面直角坐标系中,△ABC的三个顶点都在小正方形的顶点处,请结合图完成下列各题: