题目内容
4.已知关于x的不等式组$\left\{\begin{array}{l}{5x+2>3(x-1)}\\{\frac{1}{2}x≤8-\frac{3}{2}x+2a}\end{array}\right.$有四个整数解,求实数a的取值范围.分析 分别求出不等式组中两不等式的解集,根据不等式组有四个整数解,即可确定出a的范围.
解答 解:解不等式组$\left\{\begin{array}{l}{5x+2>3(x-1)}&{①}\\{\frac{1}{2}x≤8-\frac{3}{2}x+2a}&{②}\end{array}\right.$,
解不等式①得:x>-$\frac{5}{2}$,
解不等式②得:x≤a+4,
∵不等式组有四个整数解,
∴不等式组的解集再数轴上表示为:
∴1≤a+4<2,
解得:-3≤a<-2.
点评 此题考查了一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.将一根圆柱形的空心钢管任意放置,它的主视图不可能是( )
| A. |  | B. |  | C. |  | D. |  |
9.两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )
| A. | $\frac{7500}{x}$-$\frac{7500}{1.2x}$=15 | B. | $\frac{7500}{x}$-$\frac{7500}{1.2x}$=$\frac{1}{4}$ | ||
| C. | $\frac{7.5}{x}$-$\frac{7.5}{1.2x}$=15 | D. | $\frac{7.5}{x}$-$\frac{7.5}{1.2x}$=$\frac{1}{4}$ |
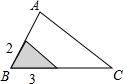
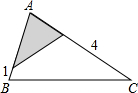
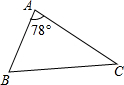 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )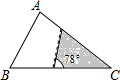

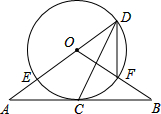 如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6. 如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: 如图,在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1=48°.
如图,在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1=48°.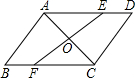 如图,AC是?ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
如图,AC是?ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.