题目内容
4.如图,平面内有一等腰直角三角形ABC(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,小明同学过点C作BF的垂线,如图1,利用三角形全等证得AF+BF=2CE.(1)若三角板绕点A顺时针旋转至图2的位置,其他条件不变,试猜想线段AF、BF、CE之间的数量关系,并证明你的猜想.
(2)若三角板绕点A顺时针旋转至图3的位置,其他条件不变,则线段AF、BF、CE之间的数量关系为BF-AF=2CE.

分析 (1)过点C作CG⊥BF,交BF延长线于点G,易证△CBG≌△CAE,根据全等三角形的对应边相等,即可证得AF+BF=2CE;
(2)过点C做CD⊥BF,交FB的于点D,易证△ACE≌△BCD,根据全等三角形的对应边相等,即可证得BF-AF=2CE.
解答 解:(1)AF-BF=2CE
图2中,过点C作CG⊥BF,交BF延长线于点G,
∵AC=BC
可得∠AEC=∠CGB,
∠ACE=∠BCG,
在△CBG和△CAE中,
$\left\{\begin{array}{l}{∠AEC=∠CGB}\\{∠ACE=∠BCG}\\{AC=BC}\end{array}\right.$,
∴△CBG≌△CAE(AAS),
∴AE=BG,
∵AF=AE+EF,
∴AF=BG+CE=BF+FG+CE=2CE+BF,
∴AF-BF=2CE;
(2)BF-AF=2CE;
如图3,过点C做CD⊥BF,交FB的于点D,
∵AC=BC
可得∠AEC=∠CDB,
∠ACE=∠BCD,
在△CBD和△CAE中,
$\left\{\begin{array}{l}{∠AEC=∠CDB}\\{∠ACE=∠BCD}\\{AC=BC}\end{array}\right.$,
∴△CBD≌△CAE(AAS),
∴AE=BD,
∵AF=AE-EF,
∴AF=BD-CE=BF-FD-CE=BF-2CE,
∴BF-AF=2CE.
故答案为:BF-AF=2CE.
点评 此题考查几何变换问题,全等三角形的判定和性质,正确作出垂线,构造全等三角形是解决本题的关键.

练习册系列答案
相关题目
12.-16的相反数是( )
| A. | -$\frac{1}{16}$ | B. | -16 | C. | $\frac{1}{16}$ | D. | 16 |
14.2015年10月18日,TCL2015长沙国际马拉松赛正式开赛,来自国内外的1.5万余名选手在长沙这座美丽的城市中奔跑.马拉松长跑是国际上非常普及的长跑比赛项目,全程距离约为42千米,将数据42千米用科学记数法表示为( )
| A. | 42×103米 | B. | 0.42×105米 | C. | 4.2×104米 | D. | 4.2×105米 |
 如图,在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1=48°.
如图,在同一平面内,将边长相等的正三角形、正五边形的一边重合,则∠1=48°.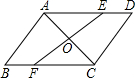 如图,AC是?ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
如图,AC是?ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F. 如图,在等腰直角△ABC中,∠ACB=90°,AC=1.
如图,在等腰直角△ABC中,∠ACB=90°,AC=1.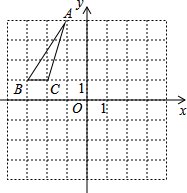 在如图所示的平面直角坐标系中,△ABC的三个顶点都在小正方形的顶点处,请结合图完成下列各题:
在如图所示的平面直角坐标系中,△ABC的三个顶点都在小正方形的顶点处,请结合图完成下列各题: