题目内容
11. 如图,∠AOC在∠AOB的内部,且∠AOB与∠AOC互补,OD平分∠AOB,OE平分∠BOC,∠DOE=20°,求∠AOB.
如图,∠AOC在∠AOB的内部,且∠AOB与∠AOC互补,OD平分∠AOB,OE平分∠BOC,∠DOE=20°,求∠AOB.
分析 根据角平分线的定义可知∠BOE=$\frac{1}{2}$∠BOC,∠BOD=$\frac{1}{2}∠AOB$,于是得到$∠DOE=\frac{1}{2}(∠AOB-∠BOC)$=$\frac{1}{2}∠AOC$,从而可求得∠AOC度数,最后根据补角的定义可求得∠AOB的度数.
解答 解:∵OD平分∠AOB,OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC,∠BOD=$\frac{1}{2}∠AOB$.
∵∠DOE=∠BOD-∠BOE,
∴∠DOE=$\frac{1}{2}(∠AOB-∠BOC)$=$\frac{1}{2}∠AOC$=20°.
解得;∠AOC=40°.
∵∠AOB与∠AOC互补,
∴∠AOB=180°-∠AOC=180°-40°=140°
点评 本题主要考查的是余角和补角、角平分线的定义,根据题意得到∠DOE=$\frac{1}{2}∠$AOC是解题的关键.

练习册系列答案
相关题目
 如图,在等腰Rt△ABC中,已知AB=BC=8cm,点P在AB上,从点A向点B方向移动,过点P作PD∥AC,交BC于D,作PE∥BC,交AC于E,问:当PA为多少厘米时,四边形PDCE的面积为15cm2?
如图,在等腰Rt△ABC中,已知AB=BC=8cm,点P在AB上,从点A向点B方向移动,过点P作PD∥AC,交BC于D,作PE∥BC,交AC于E,问:当PA为多少厘米时,四边形PDCE的面积为15cm2? 在⊙O中,AB、BC、CD为弦,∠E=60°,∠F=80°,求∠A.
在⊙O中,AB、BC、CD为弦,∠E=60°,∠F=80°,求∠A.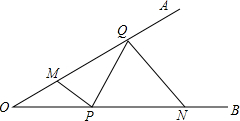 已知MN为OA、OB上的固定点,P、Q为OA、OB上的动点,在图中作出M→P→Q→N的最短路径.
已知MN为OA、OB上的固定点,P、Q为OA、OB上的动点,在图中作出M→P→Q→N的最短路径.