题目内容
1. 如图,在等腰Rt△ABC中,已知AB=BC=8cm,点P在AB上,从点A向点B方向移动,过点P作PD∥AC,交BC于D,作PE∥BC,交AC于E,问:当PA为多少厘米时,四边形PDCE的面积为15cm2?
如图,在等腰Rt△ABC中,已知AB=BC=8cm,点P在AB上,从点A向点B方向移动,过点P作PD∥AC,交BC于D,作PE∥BC,交AC于E,问:当PA为多少厘米时,四边形PDCE的面积为15cm2?
分析 设当PA为x厘米时,四边形PDCE的面积为15cm2,根据等腰三角形的性质和平行四边形的面积公式可列方程求解.
解答 解:∵PD∥AC,PE∥BC,
∴四边形PDCE为平行四边形,
∵△ABC是等腰直角三角形,AB=BC,
∴∠B=90°,∠A=∠C=45°,AC=8$\sqrt{2}$cm,
∴∠APE=90°,∠PEA=∠C,
∴∠PEA=∠A,
∴△APE是等腰直角三角形,
如图,过点P作PF⊥AE于点F,
设PA为x厘米,则AE=8$\sqrt{2}$-$\sqrt{2}$x,PF=$\frac{\sqrt{2}}{2}$x,由题意得
(8$\sqrt{2}$-$\sqrt{2}$x)$\frac{\sqrt{2}}{2}$x=15,
解得:x=5,或x=3.
答:当PA为5或3厘米时,四边形PDCE的面积为15cm2.
点评 此题主要考查了一元二次方程的应用,等腰直角三角形的性质,平行四边形的面积,找出等量关系是解决问题的关键.

练习册系列答案
相关题目
11.方程3x2+9=0的根是( )
| A. | x=-3 | B. | x=3 | C. | x=±3 | D. | 无实数根 |
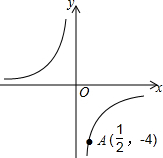 反比例函数y=$\frac{k}{x}$的图象如图所示.
反比例函数y=$\frac{k}{x}$的图象如图所示. 如图,直线AB,CD相交于点O,∠BOE:∠DOE=1:2,OF⊥OE,∠AOC=60°,求∠DOF的度数.
如图,直线AB,CD相交于点O,∠BOE:∠DOE=1:2,OF⊥OE,∠AOC=60°,求∠DOF的度数. 如图,∠AOC在∠AOB的内部,且∠AOB与∠AOC互补,OD平分∠AOB,OE平分∠BOC,∠DOE=20°,求∠AOB.
如图,∠AOC在∠AOB的内部,且∠AOB与∠AOC互补,OD平分∠AOB,OE平分∠BOC,∠DOE=20°,求∠AOB.