题目内容
16.观察下列各式的化简过程(其中a>2):①$\frac{a-2}{\sqrt{a-2}}$=$\frac{(\sqrt{a-2})^{2}}{\sqrt{a-2}}$=$\sqrt{a-2}$;
②$\frac{a-2}{\sqrt{a}-\sqrt{2}}$=$\frac{(\sqrt{a})^{2}-(\sqrt{2})^{2}}{\sqrt{a}-\sqrt{2}}$=$\frac{(\sqrt{a}+\sqrt{2})(\sqrt{a}-\sqrt{2})}{\sqrt{a}-\sqrt{2}}$=$\sqrt{a}$+$\sqrt{2}$;
③$\frac{a-4}{\sqrt{a}+2}$=$\frac{(\sqrt{a})^{2}-{2}^{2}}{\sqrt{a}+2}$=$\frac{(\sqrt{a}+2)(\sqrt{a}-2)}{\sqrt{a}+2}$=$\sqrt{a}$-2.
(1)上述各式化简过程的共同特点是:先将分子变形,通过约分.化去分母中的根号.
(2)试用上述方法化去下列各式分母中的根号.
①$\frac{2a+6}{\sqrt{a+3}}$; ②$\frac{a-1}{1+\sqrt{a}}$; ③$\frac{a-b}{\sqrt{a}-\sqrt{b}}$.
(3)你还有别的方法化去上列各式分母中的根号吗?
分析 (1)观察三个化简过程,它们的共同特点是先变形分子,使分子出现含分母的因式,然后约分可化去分母中的根号;
(2)①利用二次根式的性质把a+3写成$\sqrt{x+3}$的平方形式,然后约分即可;、
②③都是利用平方差公式把分子分解,然后约分即可;
(3)利用分式的基本性质,把分子分母都乘以分母的有理化因式可化去分母中的根号.
解答 解:(1)上述各式化简过程的共同特点是:先将分子变形,通过约分.化去分母中的根号;
故答案为分子,分母;
(2)①$\frac{2a+6}{\sqrt{a+3}}$=$\frac{2(a+3)}{\sqrt{a+3}}$=$\frac{2(\sqrt{a+3})^{2}}{\sqrt{a+3}}$=2$\sqrt{a+3}$;
②$\frac{a-1}{1+\sqrt{a}}$=$\frac{(\sqrt{a})^{2}-1}{\sqrt{a}+1}$=$\frac{(\sqrt{a}+1)(\sqrt{a}-1)}{\sqrt{a}+1}$=$\sqrt{a}$-1;
③$\frac{a-b}{\sqrt{a}-\sqrt{b}}$=$\frac{(\sqrt{a})^{2}-(\sqrt{b})^{2}}{\sqrt{a}+\sqrt{b}}$=$\frac{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}{\sqrt{a}+\sqrt{b}}$=$\sqrt{a}$-$\sqrt{b}$;
(3)把分子分母都乘以分母的有理化因式可化去上列各式分母中的根号.
点评 本题考查了分母有理化:分母有理化是指把分母中的根号化去;分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.

练习册系列答案
相关题目
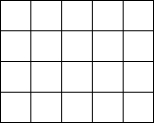 小猫在如图的地砖上随意走动,它停在任一块方砖上的机会均等,现在知道小猫停在红色方砖上的概率是$\frac{1}{4}$,试把红色方砖的颜色涂上阴影.
小猫在如图的地砖上随意走动,它停在任一块方砖上的机会均等,现在知道小猫停在红色方砖上的概率是$\frac{1}{4}$,试把红色方砖的颜色涂上阴影. 如图,∠AOC在∠AOB的内部,且∠AOB与∠AOC互补,OD平分∠AOB,OE平分∠BOC,∠DOE=20°,求∠AOB.
如图,∠AOC在∠AOB的内部,且∠AOB与∠AOC互补,OD平分∠AOB,OE平分∠BOC,∠DOE=20°,求∠AOB.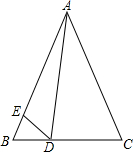 如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.△ADE与△ABD相似吗?为什么?
如图,在△ABC中,AB=AC,点D、E分别在BC、AB上,且∠BDE=∠CAD.△ADE与△ABD相似吗?为什么? 如图,直线AB∥CD,CM平分∠BCD,CN⊥CM,∠B=40°,则∠DCM=20°,∠NCD=110°,∠BCN=70°.
如图,直线AB∥CD,CM平分∠BCD,CN⊥CM,∠B=40°,则∠DCM=20°,∠NCD=110°,∠BCN=70°.
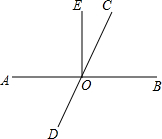 如图,已知AB,CD相交于点O,OE平分∠AOB,∠EOC=28°.
如图,已知AB,CD相交于点O,OE平分∠AOB,∠EOC=28°.