题目内容
18.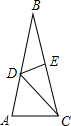 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )| A. | 30° | B. | 45° | C. | 55° | D. | 75° |
分析 根据等腰三角形的性质得到∠A=∠ACB=75°,根据线段垂直平分线的性质得到BD=CD,求得∠DCE=∠B=30°,即可得到结论.
解答 解:∵AB=BC,∠B=30°,
∴∠A=∠ACB=75°,
∵DE垂直平分BC,
∴BD=CD,
∴∠DCE=∠B=30°,
∴∠ACD=∠ACB=∠DCB=45°,
故选B.
点评 本题考查了三角形的内角和定理,等腰三角形的性质,线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列实数中,是负数的是( )
| A. | -$\sqrt{2}$ | B. | 2.5 | C. | 0 | D. | $\frac{5}{7}$ |
3.函数$y=\frac{{\sqrt{2-x}}}{x-3}$的自变量x的取值范围是( )
| A. | x≤2 | B. | x≥2且x≠3 | C. | x≥2 | D. | x≤2且x≠3 |
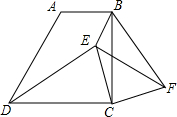 在梯形ABCD中AB∥CD,∠BCD=90°,AB=1,BC=2,tan∠ADC=2.
在梯形ABCD中AB∥CD,∠BCD=90°,AB=1,BC=2,tan∠ADC=2.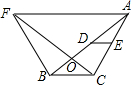 如图,△ABC是钝角三角形,DE是△ABC的中位线,现有△FCB≌△ABC,恰有AB⊥FC,垂足为O,连接AF,若DE=1.5,AF=7,则BC与AF之间的距离为5.
如图,△ABC是钝角三角形,DE是△ABC的中位线,现有△FCB≌△ABC,恰有AB⊥FC,垂足为O,连接AF,若DE=1.5,AF=7,则BC与AF之间的距离为5.