题目内容
3.函数$y=\frac{{\sqrt{2-x}}}{x-3}$的自变量x的取值范围是( )| A. | x≤2 | B. | x≥2且x≠3 | C. | x≥2 | D. | x≤2且x≠3 |
分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:根据题意得:2-x≥0且x-3≠0,
解得:x≤2且x≠3,
自变量的取值范围x≤2,
故选A.
点评 本题考查了函数自变量的取值范围问题,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
14.下列变形正确的是( )
| A. | (-3a3)2=-9a5 | B. | 2x2y-2xy2=0 | ||
| C. | -$\frac{3b}{a}$÷2ab=-$\frac{3}{2{a}^{2}}$ | D. | (2x+y)(x-2y)=2x2-2y2 |
18.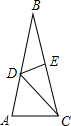 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )| A. | 30° | B. | 45° | C. | 55° | D. | 75° |
15.把-3$\sqrt{\frac{a}{3}}$根号外的因式移到根号内,所得的结果正确的是( )
| A. | -$\sqrt{a}$ | B. | -$\sqrt{-a}$ | C. | -$\sqrt{3a}$ | D. | $\sqrt{3a}$ |
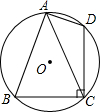 如图,△ABC内接于⊙O,弦DC⊥BC,已知⊙O的半径为5cm,弦BC长为6cm,则tan∠BAC=$\frac{3}{4}$.
如图,△ABC内接于⊙O,弦DC⊥BC,已知⊙O的半径为5cm,弦BC长为6cm,则tan∠BAC=$\frac{3}{4}$. 如图所示,能判定直线AB∥CD的条件是∠5+∠6=180°或者∠2+∠3=180°或者∠1+∠4=180°.
如图所示,能判定直线AB∥CD的条件是∠5+∠6=180°或者∠2+∠3=180°或者∠1+∠4=180°.