题目内容
7.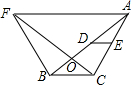 如图,△ABC是钝角三角形,DE是△ABC的中位线,现有△FCB≌△ABC,恰有AB⊥FC,垂足为O,连接AF,若DE=1.5,AF=7,则BC与AF之间的距离为5.
如图,△ABC是钝角三角形,DE是△ABC的中位线,现有△FCB≌△ABC,恰有AB⊥FC,垂足为O,连接AF,若DE=1.5,AF=7,则BC与AF之间的距离为5.
分析 过点O作GH⊥AF交AF于G,交BC于H,根据全等三角形的性质得到OB=OC,OF=OA,根据三角形中位线定理求出BC即可.
解答 解:过点O作GH⊥AF交AF于G,交BC于H,
∵DE是△ABC的中位线,DE=1.5,
∴BC=3,
∵△FCB≌△ABC,
∴∠OBC=∠OCB,FC=AB,
∴OB=OC,OF=OA,
∴OG=$\frac{1}{2}$AF=3.5,OH=$\frac{1}{2}$BC=1.5,
∴GH=5,
故答案为:5.
点评 本题考查的是三角形中位线定理和全等三角形的性质,三角形的中位线平行于第三边,并且等于第三边的一半、全等三角形的对应边相等.

练习册系列答案
相关题目
18.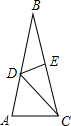 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )| A. | 30° | B. | 45° | C. | 55° | D. | 75° |
15.把-3$\sqrt{\frac{a}{3}}$根号外的因式移到根号内,所得的结果正确的是( )
| A. | -$\sqrt{a}$ | B. | -$\sqrt{-a}$ | C. | -$\sqrt{3a}$ | D. | $\sqrt{3a}$ |
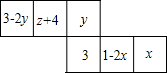 如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值.
如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值. 如图所示,能判定直线AB∥CD的条件是∠5+∠6=180°或者∠2+∠3=180°或者∠1+∠4=180°.
如图所示,能判定直线AB∥CD的条件是∠5+∠6=180°或者∠2+∠3=180°或者∠1+∠4=180°.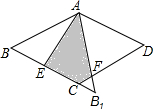 如图,在边长为$\sqrt{2}$的菱形ABCD中,∠B=45°,AE是BC边上的高,将△AEB沿AE所在直线翻折得△AEB1,则△AEB1与四边形AECF重叠部分的面积为$\sqrt{2}$-1.
如图,在边长为$\sqrt{2}$的菱形ABCD中,∠B=45°,AE是BC边上的高,将△AEB沿AE所在直线翻折得△AEB1,则△AEB1与四边形AECF重叠部分的面积为$\sqrt{2}$-1.