题目内容
8.观察下列等式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$将以上三个等式两边分别相加得:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$
(1)按照一定规律排列式子:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…,其中第n项(n为正整数)的形式为$\frac{1}{n(n+1)}$,按照材料中的写法,该项可表示为$\frac{1}{n}$-$\frac{1}{n+1}$.
(2)直接写出下式:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2009×2010}$的计算结果为$\frac{2009}{2010}$.
(3)探究并计算:$\frac{1}{2×4}$+$\frac{1}{4×6}$+…+$\frac{1}{2n×2(n+1)}$(其中n为正整数).
分析 (1)归纳总结得到一般性规律,写出第n项,表示出变形结果即可;
(2)原式利用得出的规律变形,计算即可得到结果;
(3)原式利用得出的规律变形,计算即可得到结果.
解答 解:(1)第n项为$\frac{1}{n(n+1)}$,可表示为$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…=$\frac{1}{2009}$-$\frac{1}{2010}$=1-$\frac{1}{2010}$=$\frac{2009}{2010}$;
(3)原式=$\frac{1}{2}$[$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2n}$-$\frac{1}{2(n+1)}$]=$\frac{n}{4(n+1)}$.
故答案为:(1)$\frac{1}{n(n+1)}$,$\frac{1}{n}$-$\frac{1}{n+1}$;(2)$\frac{2009}{2010}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.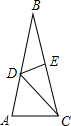 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )| A. | 30° | B. | 45° | C. | 55° | D. | 75° |
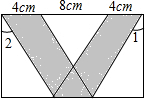 如图,在一个矩形中,有一个“V”字型的阴影图形,两个平行四边形交叉放在一起,∠1=∠2=30°,则阴影部分的面积S=44$\sqrt{3}$cm2.
如图,在一个矩形中,有一个“V”字型的阴影图形,两个平行四边形交叉放在一起,∠1=∠2=30°,则阴影部分的面积S=44$\sqrt{3}$cm2.
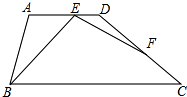 如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点F在DC上,且∠BEF=∠A.
如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点F在DC上,且∠BEF=∠A.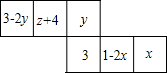 如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值.
如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式相等,求x,y,z的值.