题目内容
13.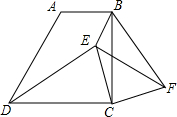 在梯形ABCD中AB∥CD,∠BCD=90°,AB=1,BC=2,tan∠ADC=2.
在梯形ABCD中AB∥CD,∠BCD=90°,AB=1,BC=2,tan∠ADC=2.(1)求证:BC=CD;
(2)E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△EFC的形状,并证明;
(3)在(2)的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.
分析 (1)此题要证明DC=BC不能用全等三角形的性质,利用tan∠ADC=2求出BC然后再判定相等;
(2)容易证明△DEC≌△BFC,得CE=CF,∠ECD=∠FCB,这样容易证明△ECF是等腰直角三角形;
(3)由∠BEC=135°得∠BEF=90°,这样求sin∠BFE,然后利用已知条件就可以求出它的值了.
解答 解:(1)如图,过A作DC的垂线AM交DC于M,则AM=BC=2.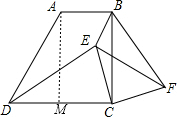
又tan∠ADC=2,
∴DM=$\frac{2}{2}$=1,
即DC=BC;
(2)等腰直角三角形.
证明:在△DEC和△BFC中,
$\left\{\begin{array}{l}{DE=BF}\\{∠EDC=∠FBC}\\{DC=BC}\end{array}\right.$,
∴△DEC≌△BFC,
∴CE=CF,∠ECD=∠FCB,
∴∠ECF=∠FCB+∠BCE=∠ECD+∠BCE=∠BCD=90°,
即△ECF是等腰直角三角形;
(3)设BE=k,则CE=CF=2k,
∴EF=2$\sqrt{2}$k,
∵∠BEC=135°,又∠CEF=45°,
∴∠BEF=90°,
所以BF=$\sqrt{{k}^{2}+(2\sqrt{2}k)^{2}}$=3k,
所以sin∠BFE=$\frac{k}{3k}=\frac{1}{3}$.
点评 本题考查三角函数、全等三角形的应用、等腰三角形的判定等知识点的综合应用及推理能力、运算能力,解决本题的关键是作出辅助线.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
4.学习完一次函数后,小荣遇到过这样的一个新颖的函数:y=|x-1|,小荣根据学校函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小荣的探究过程,请补充完成:
(1)列表:下表是y与x的几组对应值,请补充完整.
(2)描点连线:在平面直角坐标系xOy中,请描出以上表中各对对应值为坐标的点,画出该函数的图象;
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合函数的图象,写出该函数的其他性质(一条即可):当x<0时,y随x的增大而减小.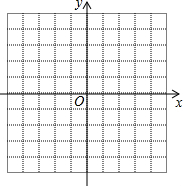
(1)列表:下表是y与x的几组对应值,请补充完整.
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 4 | 3 | 2 | 1 | 0 | 1 | 2 | … |
(3)进一步探究发现,该函数图象的最低点的坐标是(1,0),结合函数的图象,写出该函数的其他性质(一条即可):当x<0时,y随x的增大而减小.

1.下列计算正确的是( )
| A. | a-(2a-b)=-a-b | B. | (a2-2ab+a)÷a=a-2b | ||
| C. | ${({-\frac{1}{3}{a^2}})^3}=-\frac{1}{9}{a^6}$ | D. | (a+2b)(a-b)=a2+ab-2b2 |
18.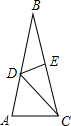 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
 如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )
如图,在△ABC中,AB=BC,∠B=30°,DE垂直平分BC,则∠ACD的度数为( )| A. | 30° | B. | 45° | C. | 55° | D. | 75° |
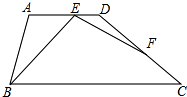 如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点F在DC上,且∠BEF=∠A.
如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点F在DC上,且∠BEF=∠A.
 如图所示,DE是△ABC的中位线,则△ADE与△ABC的周长比为1:2.
如图所示,DE是△ABC的中位线,则△ADE与△ABC的周长比为1:2.