题目内容
10．给出4个判断：①所有的等腰三角形都相似，
②所有的等边三角形都相似，
③所有的直角三角形都相似，
④所有的等腰直角三角形都相似．
其中判断正确的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 由相似三角形的判定方法得出①③不正确；②④正确；即可得出结论．
解答 解：∵所有的等腰三角形不一定相似，
∴①不正确；
∵所有的等边三角形都相似，
∴②正确；
∵所有的直角三角形不一定相似，
∴③不正确；
∵所有的等腰直角三角形都相似，
∴④正确；正确的个数有2个，
故选：B．
点评 本题考查了相似三角形的判定；熟记两角相等的两个三角形相似是解决问题的关键．
练习册系列答案
相关题目
1．下列计算正确的是（ ）
| A． | a-（2a-b）=-a-b | B． | （a2-2ab+a）÷a=a-2b | ||
| C． | ${（{-\frac{1}{3}{a^2}}）^3}=-\frac{1}{9}{a^6}$ | D． | （a+2b）（a-b）=a2+ab-2b2 |
18．
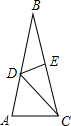如图，在△ABC中，AB=BC，∠B=30°，DE垂直平分BC，则∠ACD的度数为（ ）
如图，在△ABC中，AB=BC，∠B=30°，DE垂直平分BC，则∠ACD的度数为（ ）| A． | 30° | B． | 45° | C． | 55° | D． | 75° |
15．把-3$\sqrt{\frac{a}{3}}$根号外的因式移到根号内，所得的结果正确的是（ ）
| A． | -$\sqrt{a}$ | B． | -$\sqrt{-a}$ | C． | -$\sqrt{3a}$ | D． | $\sqrt{3a}$ |
20．下列分式中是最简分式的是（ ）
| A． | $\frac{x-1}{{{x^2}-1}}$ | B． | $\frac{4}{2x}$ | C． | $\frac{2x}{{{x^2}-1}}$ | D． | $\frac{1-x}{x-1}$ |