题目内容
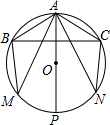 如图,在⊙O中,AP为圆的直径,弦AB=AC,AM=AN,连接BM,CN,连接BC,分别交AM,AN,AP于点E,F,N.
如图,在⊙O中,AP为圆的直径,弦AB=AC,AM=AN,连接BM,CN,连接BC,分别交AM,AN,AP于点E,F,N.(1)写出图中3对全等三角形;
(2)在①所写出的全等三角形中,选择1对加以证明.
考点:全等三角形的判定,圆周角定理
专题:
分析:由弦AB=AC,AM=AN,证出
=
,
=
,得出
=
,根据圆周角定理得出相等的角,容易证出三对三角形全等.
 |
| AB |
 |
| AC |
 |
| AM |
 |
| AN |
 |
| BM |
 |
| CN |
解答:解:(1)如图所示: △ABM≌△ACN,△ABD≌ACE,△ABE≌△ACD;
△ABM≌△ACN,△ABD≌ACE,△ABE≌△ACD;
(2)证明△ABM≌△ACN;
∵AB=AC,AM=AN,
∴
=
,
=
,
∴
=
,∠M=∠N,
∴∠BAM=∠CAN,
在△ABM和△ACN中,
∴△ABM≌△ACN(AAS).
 △ABM≌△ACN,△ABD≌ACE,△ABE≌△ACD;
△ABM≌△ACN,△ABD≌ACE,△ABE≌△ACD;(2)证明△ABM≌△ACN;
∵AB=AC,AM=AN,
∴
 |
| AB |
 |
| AC |
 |
| AM |
 |
| AN |
∴
 |
| BM |
 |
| CN |
∴∠BAM=∠CAN,
在△ABM和△ACN中,
|
∴△ABM≌△ACN(AAS).
点评:本题考查了全等三角形的判定和圆周角定理;三角形全等的判定是中考的热点,本题利用圆周角定理证出角相等是证明三角形全等的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 由半圆和直角三角形组成的图形如图,阴影Ⅰ与阴影Ⅱ这两部分,哪一个面积较大?大多少?
由半圆和直角三角形组成的图形如图,阴影Ⅰ与阴影Ⅱ这两部分,哪一个面积较大?大多少? 已知在矩形ABCD中,E是AB上一点,EF⊥CE交AD于点F,BE=2,EF=CE,矩形ABCD的周长为16.求BC的长.
已知在矩形ABCD中,E是AB上一点,EF⊥CE交AD于点F,BE=2,EF=CE,矩形ABCD的周长为16.求BC的长. 已知,如图,在矩形ABCD中,点E,F在边AB上,且AF=BE,求证:DE=CF.
已知,如图,在矩形ABCD中,点E,F在边AB上,且AF=BE,求证:DE=CF. 已知如图,在菱形ABCD中,AC,BD相交于点O,在图中有几个直角三角形?分别是哪些?
已知如图,在菱形ABCD中,AC,BD相交于点O,在图中有几个直角三角形?分别是哪些? 已知:如图,点B、F、C、E在一条直线上,∠A=∠D,AC=DF且AC∥DF
已知:如图,点B、F、C、E在一条直线上,∠A=∠D,AC=DF且AC∥DF
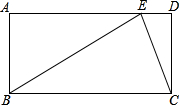 如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.
如图,矩形ABCD中,E是AD上一点,BC=BE=2CD,求∠DCE的度数.