题目内容
 已知在矩形ABCD中,E是AB上一点,EF⊥CE交AD于点F,BE=2,EF=CE,矩形ABCD的周长为16.求BC的长.
已知在矩形ABCD中,E是AB上一点,EF⊥CE交AD于点F,BE=2,EF=CE,矩形ABCD的周长为16.求BC的长.考点:全等三角形的判定与性质
专题:
分析:如图,证明△AEF≌△BCE,得到AE=BC(设为λ),AB=λ+2;由题意得2(λ+λ+2)=16,求出λ即可解决问题.
解答: 解:如图,∵四边形为矩形,
解:如图,∵四边形为矩形,
∴∠A=∠B=90°,而∠CEF=90°,
∠AFE+∠AEF=∠AEF+∠BEC,
∴∠AFE=∠BEC;
在△AEF与△BCE,
,
∴△AEF≌△BCE(AAS),
∴AE=BC(设为λ),AB=λ+2;
∵矩形ABCD的周长为16,
∴2(λ+λ+2)=16,解得:λ=3,
即BC的长为3.
 解:如图,∵四边形为矩形,
解:如图,∵四边形为矩形,∴∠A=∠B=90°,而∠CEF=90°,
∠AFE+∠AEF=∠AEF+∠BEC,
∴∠AFE=∠BEC;
在△AEF与△BCE,
|
∴△AEF≌△BCE(AAS),
∴AE=BC(设为λ),AB=λ+2;
∵矩形ABCD的周长为16,
∴2(λ+λ+2)=16,解得:λ=3,
即BC的长为3.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;应牢固掌握全等三角形的判定,这是灵活解题的基础和关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,已知两棵小树在同一时刻的影子,请画出此时的光线,并指出影子是在什么光线下形成的?
如图,已知两棵小树在同一时刻的影子,请画出此时的光线,并指出影子是在什么光线下形成的?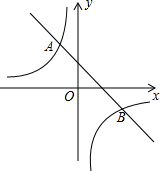 已知:如图,一次函数y=kx+b的图象与反比例函数y=
已知:如图,一次函数y=kx+b的图象与反比例函数y= 某校的校园内有一个由两个相同的正六边形(边长为2.5m)围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示,并在新扩充的部分种上草坪,则扩建后菱形区域的周长为( )
某校的校园内有一个由两个相同的正六边形(边长为2.5m)围成的花坛,如图中的阴影部分所示,校方先要将这个花坛在原有的基础上扩建成一个菱形区域如图所示,并在新扩充的部分种上草坪,则扩建后菱形区域的周长为( ) 小颖将手中的一副三角尺按如图所示摆放在一起,连接AD后,你能帮他求出∠ADB的正切值吗?
小颖将手中的一副三角尺按如图所示摆放在一起,连接AD后,你能帮他求出∠ADB的正切值吗?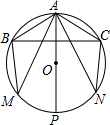 如图,在⊙O中,AP为圆的直径,弦AB=AC,AM=AN,连接BM,CN,连接BC,分别交AM,AN,AP于点E,F,N.
如图,在⊙O中,AP为圆的直径,弦AB=AC,AM=AN,连接BM,CN,连接BC,分别交AM,AN,AP于点E,F,N. 如图,在∠1、∠2、∠3、∠4中,同位角为
如图,在∠1、∠2、∠3、∠4中,同位角为