题目内容
已知，如图，在矩形ABCD中，点E，F在边AB上，且AF=BE，求证：DE=CF．考点：矩形的性质
专题：证明题
分析：根据矩形的性质可得∠A=∠B，AD=BC，然后根据SAS证明△ADE≌△BCF，然后根据全等三角形的对应边相等证明．
解答：证明：∵AF=BE，
∴AE=BF．
又∵矩形ABCD中，AD=BC，∠A=∠B=90°，
在△ADE和△BCF中，
，
∴△ADE≌△BCF（SAS）．
∴DE=CF．
∴AE=BF．
又∵矩形ABCD中，AD=BC，∠A=∠B=90°，
在△ADE和△BCF中，
|
∴△ADE≌△BCF（SAS）．
∴DE=CF．
点评：本题考查了矩形的性质以及全等三角形的判定与性质，证明线段相等的问题最常用的方法是证明三角形全等．
练习册系列答案
相关题目
光线由上到下照射一个三棱柱时的正投影如图所示，三棱柱的高为10，请分别画出三棱柱的各个侧面的正投影，并标出投影的边长．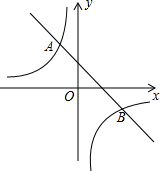
已知：如图，一次函数y=kx+b的图象与反比例函数y=
小颖将手中的一副三角尺按如图所示摆放在一起，连接AD后，你能帮他求出∠ADB的正切值吗？
如图，点O在直线AB上，∠AOD沿直线OD翻折得到∠COD，OE是∠BOC的平分线，说明OD⊥OE的理由．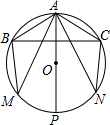
如图，在⊙O中，AP为圆的直径，弦AB=AC，AM=AN，连接BM，CN，连接BC，分别交AM，AN，AP于点E，F，N．