题目内容
 已知如图,在菱形ABCD中,AC,BD相交于点O,在图中有几个直角三角形?分别是哪些?
已知如图,在菱形ABCD中,AC,BD相交于点O,在图中有几个直角三角形?分别是哪些?(1)若∠BAD=60°,则∠BAC,∠ABD分别是多少?
(2)若AC=6,BD=8,则菱形的面积、周长是多少?
考点:菱形的性质
专题:
分析:(1)根据菱形的性质直接得出图中直角三角形的个数,再根据菱形的对角线互相垂直且平分和∠BAD=60°,得出∠BAC的度数,再根据菱形的四边相等,即可得出∠ABD的度数;
(2)根据菱形的面积是对角线乘积的一半可直接得出菱形ABCD的面积,再根据菱形的对角线互相垂直且平分和勾股定理求出菱形的一边的长,再根据菱形的四边相等即可得出菱形的周长.
(2)根据菱形的面积是对角线乘积的一半可直接得出菱形ABCD的面积,再根据菱形的对角线互相垂直且平分和勾股定理求出菱形的一边的长,再根据菱形的四边相等即可得出菱形的周长.
解答:解:在图中有四个直角三角形,分别是△AOD,△AOB,△BOC,△DOC;
(1)∵四边形ABCD是菱形,∠BAD=60°,
∴∠BAC=30°,AB=AD,
∴∠ABD=∠ADO,
∴∠ABD=60°;
(2)∵AC=6,BD=8,
∴菱形的面积是:
=24,
∵ABCD是菱形,
∴OB=4,AO=3,
∴AB=5,
∴菱形ABCD的周长是:5×4=20.
(1)∵四边形ABCD是菱形,∠BAD=60°,
∴∠BAC=30°,AB=AD,
∴∠ABD=∠ADO,
∴∠ABD=60°;
(2)∵AC=6,BD=8,
∴菱形的面积是:
| 6×8 |
| 2 |
∵ABCD是菱形,
∴OB=4,AO=3,
∴AB=5,
∴菱形ABCD的周长是:5×4=20.
点评:此题考查了菱形的性质,注意掌握菱形的四边相等,对角线互相垂直且平分,面积是对角线乘积的一半.

练习册系列答案
相关题目
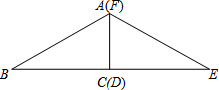 如图,Rt△ABC≌Rt△FED,其中∠BCA=∠EDF=90°,∠B=∠E=30°,AC=FD=
如图,Rt△ABC≌Rt△FED,其中∠BCA=∠EDF=90°,∠B=∠E=30°,AC=FD= 小颖将手中的一副三角尺按如图所示摆放在一起,连接AD后,你能帮他求出∠ADB的正切值吗?
小颖将手中的一副三角尺按如图所示摆放在一起,连接AD后,你能帮他求出∠ADB的正切值吗? 如图,点O在直线AB上,∠AOD沿直线OD翻折得到∠COD,OE是∠BOC的平分线,说明OD⊥OE的理由.
如图,点O在直线AB上,∠AOD沿直线OD翻折得到∠COD,OE是∠BOC的平分线,说明OD⊥OE的理由.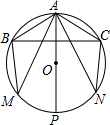 如图,在⊙O中,AP为圆的直径,弦AB=AC,AM=AN,连接BM,CN,连接BC,分别交AM,AN,AP于点E,F,N.
如图,在⊙O中,AP为圆的直径,弦AB=AC,AM=AN,连接BM,CN,连接BC,分别交AM,AN,AP于点E,F,N. 如图,设∠XOY=α
如图,设∠XOY=α
 已知,如图,在?ABCD中,E,F分别是BC,AD的中点,AE,BF相交于点G,DE,CF相交于点H,求证:GH∥AD且GH=
已知,如图,在?ABCD中,E,F分别是BC,AD的中点,AE,BF相交于点G,DE,CF相交于点H,求证:GH∥AD且GH=