题目内容
5.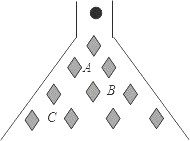 在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
分析 画出树状图,然后根据树状图即可求得小球下落到第三层B位置处的概率.
解答 解:∵实心小球在碰到菱形挡块时向左或向右下落是等可能性的,
∴经过一个菱形挡块后向左或向右下落的概率各是原概率的一半.
画树状图如下: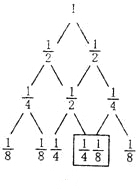
所以落到B点位置的概率为:$\frac{1}{2}$+$\frac{1}{4}$=$\frac{5}{8}$.
故答案为:$\frac{5}{8}$.
点评 此题考查了树状图法求率.此题难度较大,解题的关键是理解题意,然后根据题意画出树状图,然后利用树状图求得概率,注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14.完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完全这件事的不同办法数是各类不同方法种树的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分别几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分布计数原理,也叫做乘法原理.
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
小王想获得至少30分的加分,那么概率为多少?
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
| 加分 | 人数 |
| 10 | 30 |
| 20 | 90 |
| 30 | 150 |
| 60 | 30 |
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交$\widehat{AB}$于点E,以点C为圆心,OA的长为直径作半圆交OE于点D.若OA=4,则图中阴影部分的面积为$\frac{5π}{3}$-2$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交$\widehat{AB}$于点E,以点C为圆心,OA的长为直径作半圆交OE于点D.若OA=4,则图中阴影部分的面积为$\frac{5π}{3}$-2$\sqrt{3}$. 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB. 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BO的延长线交⊙O于C、D.若⊙O的半径为1,求四边形ABCD的面积最小值.
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BO的延长线交⊙O于C、D.若⊙O的半径为1,求四边形ABCD的面积最小值.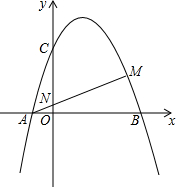 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,M为第一象限的抛物线上一点,AM交y轴于N,且AM•AN=4.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,M为第一象限的抛物线上一点,AM交y轴于N,且AM•AN=4.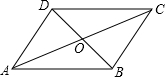 如图,在平行四边形ABCD中,O是对角线AC,BD的交点
如图,在平行四边形ABCD中,O是对角线AC,BD的交点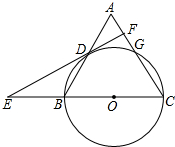 如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.
如图,在△ABC中,CA=CB,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.