题目内容
13.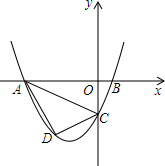 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
分析 (1)根据OC=3OB,B(1,0),求出C点坐标(0,-3),把点B,C的坐标代入y=ax2+2ax+c,求出a点坐标即可求出函数解析式;
(2)过点D作DE∥y轴分别交线段AC于点E.设D(m,m2+2m-3),然后求出DE的表达式,把S四边形ABCD分解为S△ABC+S△ACD,转化为二次函数求最值;
(3)①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形.②平移直线AC交x轴于点E,交x轴上方的抛物线于点P2,P3,由题意可知点P2、P3的纵坐标为3,从而可求得其横坐标.
解答 解:(1)∵B的坐标为(1,0),
∴OB=1.
∵OC=3OB=3,点C在x轴下方,
∴C(0,-3).
∵将B(1,0),C(0,-3)代入抛物线的解析式得:$\left\{\begin{array}{l}{4a+c=0}\\{c=-3}\end{array}\right.$,解得:a=$\frac{3}{4}$,C=-3,
∴抛物线的解析式为y=$\frac{3}{4}$x2+$\frac{9}{4}$x-3.
(2)如图1所示:过点D作DE∥y,交AC于点E.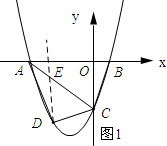
∵x=-$\frac{b}{2a}$=$\frac{-\frac{9}{4}}{2×\frac{3}{4}}$=-$\frac{3}{2}$,B(1,0),
∴A(-4,0).
∴AB=5.
∴S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×5×3=7.5.
设AC的解析式为y=kx+b.
∵将A(-4,0)、C(0,-3)代入得:$\left\{\begin{array}{l}{-4k+b=0}\\{b=-3}\end{array}\right.$,解得:k=-$\frac{3}{4}$,b=-3,
∴直线AC的解析式为y=-$\frac{3}{4}$x-3.
设D(a,$\frac{3}{4}$a2+$\frac{9}{4}$a-3),则E(a,-$\frac{3}{4}$a-3).
∵DE=-$\frac{3}{4}$a-3-($\frac{3}{4}$a2+$\frac{9}{4}$a-3)=-$\frac{3}{4}$(a+2)2+3,
∴当a=-2时,DE有最大值,最大值为3.
∴△ADC的最大面积=$\frac{1}{2}$DE•AO=$\frac{1}{2}$×3×4=6.
∴四边形ABCD的面积的最大值为13.5.
(3)存在.
①如图2,过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形.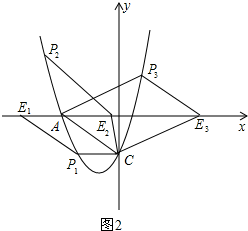
∵C(0,-3),令$\frac{3}{4}$x2+$\frac{9}{4}$x-3=-3,
∴x1=0,x2=-3.
∴P1(-3,-3).
②平移直线AC交x轴于点E2,E3,交x轴上方的抛物线于点P2,P3,当AC=P2E2时,四边形ACE2P2为平行四边形,当AC=P3E3时,四边形ACE3P3为平行四边形.
∵C(0,-3),
∴P2,P3的纵坐标均为3.
令y=3得:$\frac{3}{4}$x2+$\frac{9}{4}$x-3=3,解得;x1=$\frac{-3-\sqrt{41}}{2}$,x2=$\frac{-3+\sqrt{41}}{2}$.
∴P2($\frac{-3-\sqrt{41}}{2}$,3),P3($\frac{-3+\sqrt{41}}{2}$,3).
综上所述,存在3个点符合题意,坐标分别是:P1(-3,-3),P2($\frac{-3-\sqrt{41}}{2}$,3),P3($\frac{-3+\sqrt{41}}{2}$,3).
点评 本题考查了二次函数综合题,涉及待定系数法求二次函数的解析式,二次函数求最值,平行四边形的判定与性质等知识,根据题意作出图形,利用数形结合求解是解答此题的关键,在解答(3)时要注意进行分类讨论.

 寒假学与练系列答案
寒假学与练系列答案| A. | m≠2 | B. | m≠-1 | C. | m=-1 | D. | m≠2且m≠-1 |
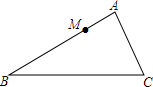 在△ABC中,AB=9,AC=6.点M在边AB上,且AM=3,点N在AC边上.当AN=2或4.5时,△AMN与原三角形相似.
在△ABC中,AB=9,AC=6.点M在边AB上,且AM=3,点N在AC边上.当AN=2或4.5时,△AMN与原三角形相似.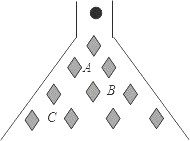 在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.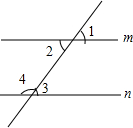 如图,请写出一个能使m∥n的条件∠2=∠3.
如图,请写出一个能使m∥n的条件∠2=∠3.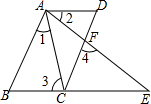 如图,若AB∥CD,∠1=∠2,∠3=∠4,AD与BC平行吗?并请说明理由.
如图,若AB∥CD,∠1=∠2,∠3=∠4,AD与BC平行吗?并请说明理由.