题目内容
10.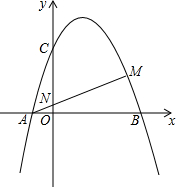 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,M为第一象限的抛物线上一点,AM交y轴于N,且AM•AN=4.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,M为第一象限的抛物线上一点,AM交y轴于N,且AM•AN=4.(1)求证:AM⊥BM;
(2)求点M的坐标.
分析 (1)根据抛物线与x轴的交点坐标,求出点A,B的坐标,根据两边成比例且夹角相等,由AM•AN=AO•AB,证明△AON∽△AMB,进而证得结论;
(2)设点M的坐标为(m,-m2+2m+3),根据两角相等的两个三角形相似,证明△AMD∽△MBD,可得$\frac{MD}{AD}=\frac{DB}{DM}$,即可解答.
解答 (1)证明:在y=-x2+2x+3中令y=0,解得x=-1或3.
则A的坐标是(-1,0),B的坐标是(3,0).
则OA=1,AB=1+3=4.OA•AB=1×4=4,
∵AM•AN=4,
∴AM•AN=AO•AB,
∴$\frac{AO}{AM}$=$\frac{AN}{AB}$,
又∵∠NAO=∠BAM,
∴△AON∽△AMB,
∴∠AMB=∠AON=90°,
∴AM⊥BM;
(2)解:连接BM,过点M作MD⊥x轴于点D,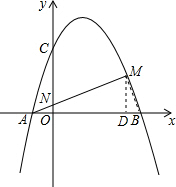
由(1)可知,∠AMD+∠DMB=90°,
∵MD⊥x轴,
∴∠AMD+∠DAM=90°,
∴∠DMB=∠DAM,
∵∠AMB=∠ADM=90°,
∴△AMD∽△MBD,
∴$\frac{MD}{AD}=\frac{DB}{DM}$,即DM2=DB•AD,
设点M的坐标为(m,-m2+2m+3),
∴(-m2+2m+3)2=(m+1)(3-m),解得:m1=3,m2=-1,m3=$1+\sqrt{3}$,m4=$1-\sqrt{3}$,
∵点M在第一象限,
∴m1=3,m2=-1,m4=$1-\sqrt{3}$,不合题意,都舍去,
∴m=$1+\sqrt{3}$,
∴-m2+2m+3=1,
即点M($1+\sqrt{3}$,1).
点评 本题主要考查抛物线与x轴的交点及三角形相似的性质和判定,解决第(2)小题时,关键是能准确找到相似三角形.

练习册系列答案
相关题目
11.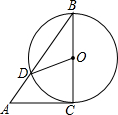 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )| A. | 100° | B. | 80° | C. | 50° | D. | 40° |
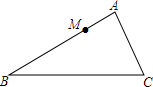 在△ABC中,AB=9,AC=6.点M在边AB上,且AM=3,点N在AC边上.当AN=2或4.5时,△AMN与原三角形相似.
在△ABC中,AB=9,AC=6.点M在边AB上,且AM=3,点N在AC边上.当AN=2或4.5时,△AMN与原三角形相似.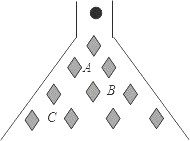 在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.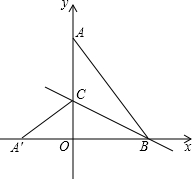 如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,求直线BC的解析式.
如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,求直线BC的解析式.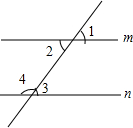 如图,请写出一个能使m∥n的条件∠2=∠3.
如图,请写出一个能使m∥n的条件∠2=∠3.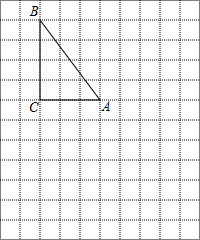 在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,
在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,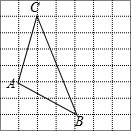 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.