题目内容
17.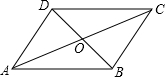 如图,在平行四边形ABCD中,O是对角线AC,BD的交点
如图,在平行四边形ABCD中,O是对角线AC,BD的交点(1)若CD=10cm,AD=6cm,OD的取值范围是2<OD<8;
(2)四边形ABCD的周长为36cm,而△COD的周长比△AOD的周长多4cm,则AB=11cm.
分析 (1)由平行四边形的性质得出AD=BC,OD=OB=$\frac{1}{2}$BD,OA=OC,AB=CD=10cm,由三角形的三边关系得出4<BD<16,即可得出结果;
(2)由平行四边形的周长得出CD+AD=18cm①,由三角形的周长关系得出CD-AD=4cm②,求出CD=11cm,即可得出AB.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,OD=OB=$\frac{1}{2}$BD,OA=OC,AB=CD=10cm,
在△ABD中,由三角形的三边关系得:
10-6<BD<6+10,
即4<BD<16,
∴2<OD<8;
故答案为:2<OD<8;
(2)∵四边形ABCD的周长为36cm,
∴CD+AD=18cm①,
∵△COD的周长比△AOD的周长多4cm,
∴OC+OD+CD-(OA+OD+AD)=4cm,
∴CD-AD=4cm②,
由①②得:CD=11cm,
∴AB=11cm;
故答案为:11cm.
点评 本题考查了平行四边形的性质、三角形的三边关系;熟练掌握平行四边形的性质,熟记三角形的三边关系是解决问题(1)的关键.

练习册系列答案
相关题目
5.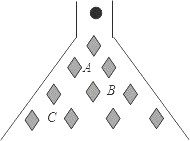 在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
 在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
9.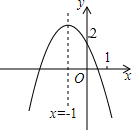 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①3a+2b+c<0;
②3a+c<b2-4ac;
③方程2ax2+2bx+2c-5=0没有实数根;
④m(am+b)+b<a(m≠-1).
其中正确结论的个数是( )
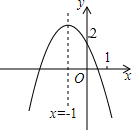 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①3a+2b+c<0;
②3a+c<b2-4ac;
③方程2ax2+2bx+2c-5=0没有实数根;
④m(am+b)+b<a(m≠-1).
其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
6.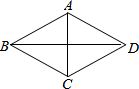 如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )
如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )
 如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )
如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )| A. | 5 | B. | 10 | C. | 5$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
 如图,△ABC三边的长分别为AB=4,BC=5,CA=6,直线l∥BC分别交△ABC的两边AB、AC于点M、N.
如图,△ABC三边的长分别为AB=4,BC=5,CA=6,直线l∥BC分别交△ABC的两边AB、AC于点M、N.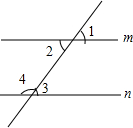 如图,请写出一个能使m∥n的条件∠2=∠3.
如图,请写出一个能使m∥n的条件∠2=∠3.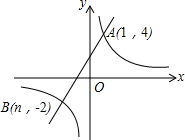 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).