题目内容
7．解不等式组$\left\{\begin{array}{l}{\frac{x}{2}＜\frac{x-1}{3}}\\{3（x+1）＞4x+2}\end{array}\right.$．分析 首先解每个不等式，两个不等式的解集的公共部分就是不等式组的解集．
解答 解：$\left\{\begin{array}{l}{\frac{x}{2}＜\frac{x-1}{3}…①}\\{3（x+1）＞4x+2…②}\end{array}\right.$，
解不等式①，得x＜-2．
解不等式②，得x＜1．
故不等式组的解集是x＜-2．
点评 本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
5．
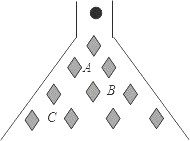在科技馆里，小亮看见一台名为帕斯卡三角的仪器，如图所示，当一实心小球从入口落下，它在依次碰到每层菱形挡块时，会等可能地向左或向右落下．试问小球下落到第三层B位置的概率是$\frac{5}{8}$．
在科技馆里，小亮看见一台名为帕斯卡三角的仪器，如图所示，当一实心小球从入口落下，它在依次碰到每层菱形挡块时，会等可能地向左或向右落下．试问小球下落到第三层B位置的概率是$\frac{5}{8}$．
6．
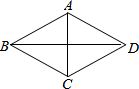如图，菱形ABCD中，AB=5，∠BCD=120°，则对角线BD的长是（ ）
如图，菱形ABCD中，AB=5，∠BCD=120°，则对角线BD的长是（ ）| A． | 5 | B． | 10 | C． | 5$\sqrt{3}$ | D． | 10$\sqrt{3}$ |