题目内容
6. 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交$\widehat{AB}$于点E,以点C为圆心,OA的长为直径作半圆交OE于点D.若OA=4,则图中阴影部分的面积为$\frac{5π}{3}$-2$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交$\widehat{AB}$于点E,以点C为圆心,OA的长为直径作半圆交OE于点D.若OA=4,则图中阴影部分的面积为$\frac{5π}{3}$-2$\sqrt{3}$.
分析 连接OE,根据CE⊥OA且OA=4可知OC=2,故cos∠EOC=$\frac{OC}{OE}$=$\frac{1}{2}$,由此可得出∠COE的度数,进而得出∠BOE的度数,根据S阴影=S扇形AOB-S扇形ACD-S扇形BOE-S△COE即可得出结论.
解答 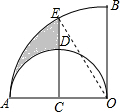 解:连接OE,
解:连接OE,
∵C为OA的中点,CE⊥OA且OA=4,
∴OC=2,
∴cos∠EOC=$\frac{OC}{OE}$=$\frac{1}{2}$,CE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴∠COE=60°.
∵∠AOB=90°,
∴∠BOE=30°,
∴S阴影=S扇形AOB-S扇形ACD-S扇形BOE-S△COE
=$\frac{90π×{4}^{2}}{360}$-$\frac{90π×{2}^{2}}{360}$-$\frac{30π×{4}^{2}}{360}$-$\frac{1}{2}$×2×2$\sqrt{3}$
=4π-π-$\frac{4π}{3}$-2$\sqrt{3}$
=$\frac{5π}{3}$-2$\sqrt{3}$.
故答案为:$\frac{5π}{3}$-2$\sqrt{3}$.
点评 本题考查的是扇形面积的计算,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求出∠COE的度数是解答此题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
16.遗爱湖有5400亩,15亩=10000平方米,用科学记数法表示遗爱湖面积为( )
| A. | 8.1×105平方米 | B. | 8.1×106平方米 | C. | 3.6×105平方米 | D. | 3.6×106平方米 |
14.函数y=(m-2)x+(m+1)是关于x的一次函数,那么m的取值范围是( )
| A. | m≠2 | B. | m≠-1 | C. | m=-1 | D. | m≠2且m≠-1 |
1.2014年11月12日正式通车的合肥高铁总投资36.32亿元,36.32亿元用科学记数法表示正确的是( )
| A. | 36.32×108 | B. | 3.632×108 | C. | 3.632×109 | D. | 0.3632×1010 |
11.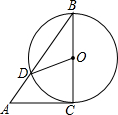 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠BAC=50°,则∠COD的大小为( )| A. | 100° | B. | 80° | C. | 50° | D. | 40° |
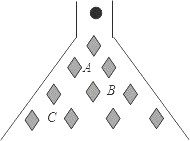 在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.