题目内容
15.一辆汽车从甲地开往乙地以80km/h的速度行驶2小时,停下来加油用了10分钟,加满之后继续行驶,到达乙地,油箱中的油刚好用完,当汽车行驶2小时时,一辆出租车正好从甲地驶往乙地,行驶2小时追上汽车,此时汽车油箱有油16L,其中汽车油箱中剩油量与行驶路程关系、两车行驶路程与时间的关系分别为图象所示,求两车何时相距20km?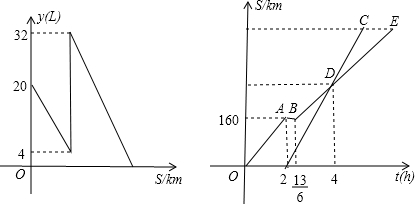
分析 由函数图象可知汽车2小时行驶的路程为160千米,耗油量为20-4-16升,所以汽车每千米耗油0.1升,出租车追上汽车时,汽车耗油32-16=16升,从而可求得点D的坐标为(4,320),然后利用待定系数法求得直线DC和直线BE的解析式,最后根据两车的相距20km列方程求解即可.
解答 解:(20-4)÷160=0.1升/千米,32-16=16升,16÷0.1=160千米,
∴点D的坐标为(4,320).
设DC的解析式为y1=k1x+b1,BE的解析式为y2=k2x+b2
将(2,0)(4,320)代入y1=k1x+b1得:$\left\{\begin{array}{l}{2{k}_{1}+{b}_{1}=0}\\{4{k}_{1}+{b}_{1}=320}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=160}\\{{b}_{1}=-320}\end{array}\right.$,
∴直线DC的解析式为y=160x-320,
将点($\frac{13}{6}$,160)(4,320)代入y2=k2x+b2得:$\left\{\begin{array}{l}{\frac{13}{6}{k}_{2}+{b}_{2}=160}\\{4{k}_{2}+{b}_{2}=320}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{k}_{2}=\frac{960}{11}}\\{{b}_{2}=-\frac{320}{11}}\end{array}\right.$,
∴直线BE的解析式为y2=$\frac{960}{11}x-\frac{320}{11}$,
∵两车相距20千米,
∴|y1-y2|=20,即:$\frac{800}{11}x-\frac{3200}{11}$=20或$\frac{800}{11}x-\frac{3200}{11}$=-20
解得x=$\frac{171}{40}$或x=$\frac{149}{40}$
答:当汽车出发$\frac{149}{40}$小时或$\frac{171}{40}$小时,两车相距20千米.
点评 本题主要考查的是一次函数的应用,跟图函数图象求得汽车每千米的耗油量,从而求得点D的坐标是解题的关键.

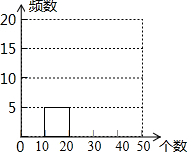 体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.
体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.| 组别 | 垫球个数x(个) | 频数(人数) |
| 1 | 10≤x<20 | 5 |
| 2 | 20≤x<30 | a |
| 3 | 30≤x<40 | 20 |
| 4 | 40≤x<50 | 16 |
(2)补全频数分布直方图;
(3)求第四组点球各所在40≤x<50的人数占被调查人数的百分比;
(4)若垫球个数在20个以上(含20个)算合格,该校七年级有400名学生,请你估计该校七年级学生在这一项目中合格的学生约有多少人?
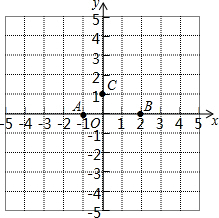 如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )| A. | (3,1) | B. | (-4,1) | C. | (1,-1) | D. | (-3,1) |
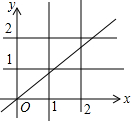 如图,若正比例函数y=kx图象与四条直线x=1,x=2,y=1,y=2相交围成的正方形有公共点,则k的取值范围是( )
如图,若正比例函数y=kx图象与四条直线x=1,x=2,y=1,y=2相交围成的正方形有公共点,则k的取值范围是( )| A. | k≤2 | B. | k≥$\frac{1}{2}$ | C. | 0<k<$\frac{1}{2}$ | D. | $\frac{1}{2}$≤k≤2 |
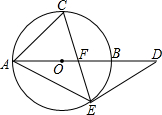 如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CE交AB于F,过E作⊙O的切线交AB的延长线于D.
如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CE交AB于F,过E作⊙O的切线交AB的延长线于D. 如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=5.则矩形的对角线长是( )
如图,矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AB=5.则矩形的对角线长是( )