题目内容
10.在等腰△ABC中,AB=AC,中线BD将三角形的周长分成了15和18两个部分,则底边长BC=9或13.分析 题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.
解答  解:设等腰三角形的底边长为x,腰长为y,则根据题意,
解:设等腰三角形的底边长为x,腰长为y,则根据题意,
得$\left\{\begin{array}{l}{x+\frac{y}{2}=15}\\{y+\frac{y}{2}=18}\end{array}\right.$或$\left\{\begin{array}{l}{x+\frac{y}{2}=18}\\{y+\frac{y}{2}=15}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=9}\\{y=12}\end{array}\right.$或$\left\{\begin{array}{l}{x=13}\\{y=10}\end{array}\right.$,
经检验,这两组解均能构成三角形,所以底边长为9或13.
故答案为:9或13.
点评 本题考查的是等腰三角形的性质,根据题意画出图形,列出关于x、y的方程组是解答此题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
5. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为( )| A. | 6 | B. | 7 | C. | 8 | D. | 不能确定 |
2.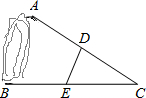 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )| A. | 280米 | B. | 300米 | C. | 420米 | D. | 无法确定 |
20. 如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
 如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{5}$ |
 如图,已知点D在双曲线y=$\frac{20}{x}$(x>0)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线y=ax2+bx+c经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
如图,已知点D在双曲线y=$\frac{20}{x}$(x>0)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线y=ax2+bx+c经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.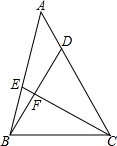 如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3.
如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3. 如图,AB∥CD,若∠1=35°,则∠2的度数为145°.
如图,AB∥CD,若∠1=35°,则∠2的度数为145°.
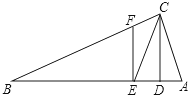 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.