题目内容
5.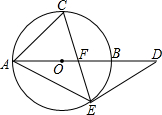 如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CE交AB于F,过E作⊙O的切线交AB的延长线于D.
如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CE交AB于F,过E作⊙O的切线交AB的延长线于D.(1)求证:DE=DF;
(2)连接AE、AC,若OF=1,OA=3,求S△ACE.
分析 (1)利用切线的性质得出∠CED=∠CAE,进而结合三角形的外角性质得出∠CED=∠DFE,求出即可;
(2)利用切线的性质以及勾股定理得出DO的长,进而利用S△ACE=S△ACF+S△AFE求出即可.
解答 (1)证明:∵AB为⊙O的直径,点C为$\widehat{AB}$的中点,
∴∠AEC=∠CAB=45°
∵DE为⊙O的切线,
∴∠CED=∠CAE,
即∠CED=∠CAB+∠BAE=45°+∠BAE,
∵∠DFE为△AEF的外角,
∴∠DEF=∠AEC+∠BAE=45°+∠BAE,
∴∠CED=∠DFE,
∴DE=DF;
(2)解:连接CO,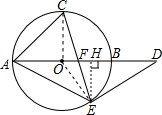 过点E作EH⊥AB于点H,连接EO,
过点E作EH⊥AB于点H,连接EO,
∵点C为$\widehat{AB}$的中点,
∴∠AOC=∠COB=90°,即CO⊥AF,
∴S△ACF=$\frac{1}{2}•AF•CO=\frac{1}{2}×4$×3=6,
∵AO=3,∴AB=6,AF=4,
∴BF=2,
∵DE=DF,
设DE=DF=x,
∵DE是⊙O的切线,则OE⊥DE,
故在Rt△OED中,EO2+DE2=DO2,
则32+x2=(x+1)2,
解得:x=4,
故EH×DO=EO×ED,
即5EH=3×4,
解得:EH=2.4,
∴S△AEF=$\frac{1}{2}$×AF×EH=$\frac{1}{2}$×4×2.4=4.8,
故S△ACE=S△ACF+S△AFE=6+4.8=10.8.
点评 此题主要考查了切线的判定与性质以及勾股定理等知识,根据S△ACE=S△ACF+S△AFE得出是解题关键.

练习册系列答案
相关题目
1. 小青在八年级上学期各次数学考试的成绩如表:
小青在八年级上学期各次数学考试的成绩如表:
(1)求小青该学期平时测验的平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,请计算出小青该学期的总评成绩.
 小青在八年级上学期各次数学考试的成绩如表:
小青在八年级上学期各次数学考试的成绩如表:| 考试类别 | 平时 | 期中考试 | 期末考试 | |||
| 测验1 | 测验2 | 测验3 | 测验4 | |||
| 成绩(分) | 132 | 105 | 146 | 129 | 134 | 130 |
(2)如果学期的总评成绩是根据图所示的权重计算,请计算出小青该学期的总评成绩.
18.在△ABC中,∠A=50°,∠B=40°,则△ABC的形状是( )
| A. | 等边三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
 如图,已知点D在双曲线y=$\frac{20}{x}$(x>0)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线y=ax2+bx+c经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
如图,已知点D在双曲线y=$\frac{20}{x}$(x>0)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线y=ax2+bx+c经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q. 如图是由边长为1的小正方形组成的网格,点A、B、C都在网格的格点上.
如图是由边长为1的小正方形组成的网格,点A、B、C都在网格的格点上.
 如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题: