题目内容
14.已知关于x的方程x2-3mx+2(m-1)=0的两根为x1、x2,且$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{3}{4}$,则m的值是多少?分析 利用根与系数的关系得到x1+x2=3m,x1x2=2(m-1),再变形已知条件得到$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{3}{4}$,则$\frac{3m}{2(m-1)}$=-$\frac{3}{4}$,然后解方程求出m,再利用判别式的意义可确定m的值.
解答 解:根据题意得x1+x2=3m,x1x2=2(m-1),
∵$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{3}{4}$,
∴$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{3}{4}$,
∴$\frac{3m}{2(m-1)}$=-$\frac{3}{4}$,
解得m=$\frac{1}{3}$,
∵△>0,
∴m的值为$\frac{1}{3}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
19.某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及 以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
表2:小王抽样调查单位10名职工的健康指数
表3:小李抽样调查单位10名职工的健康指数
根据上述材料回答问题:
(1)小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据能够较好地反映出该单位职工健康情况表,绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图.
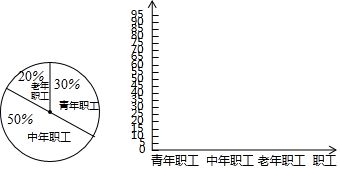
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
| 年龄 | 26 | 42 | 57 |
| 健康指数 | 97 | 79 | 72 |
| 年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
| 健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
| 年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
| 健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
(1)小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据能够较好地反映出该单位职工健康情况表,绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图.

3.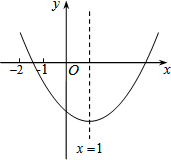 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2-4ac>0;②2a-b=0;③abc>0;④8a+c>0;⑤9a+3b+c<0,
其中正确结论的个数是( )
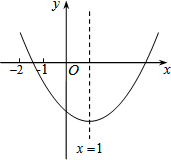 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②2a-b=0;③abc>0;④8a+c>0;⑤9a+3b+c<0,
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.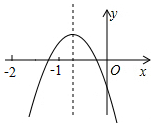 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )
 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )| A. | 4ac<b2 | B. | abc<0 | C. | b+c>3a | D. | a<b |
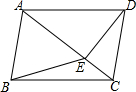 如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.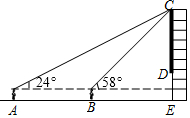 如图是某市中心一家大型购物商城墙面上的电子屏幕,好学的小希想利用所学的知识测量电子屏幕上下端之间的高度,于是她站在屏幕正前方的点A处,测得电子屏幕上端C处的仰角为24°,接着他正对电子屏幕方向前进7m到达点B处,又测得电子屏幕上端C处的仰角为58°,已知图中所有点均在同一平面内,小希的眼睛始终距离地面1.60m,CE⊥AE,DE=3m,请你根据以上测量数据,求该电子屏幕上下端之间的高度CD.(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果精确到0.1m)
如图是某市中心一家大型购物商城墙面上的电子屏幕,好学的小希想利用所学的知识测量电子屏幕上下端之间的高度,于是她站在屏幕正前方的点A处,测得电子屏幕上端C处的仰角为24°,接着他正对电子屏幕方向前进7m到达点B处,又测得电子屏幕上端C处的仰角为58°,已知图中所有点均在同一平面内,小希的眼睛始终距离地面1.60m,CE⊥AE,DE=3m,请你根据以上测量数据,求该电子屏幕上下端之间的高度CD.(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果精确到0.1m) 将边长为2的等边△OAB按如图位置放置,AB边与y轴的交点为C,则OC=$3\sqrt{2}-\sqrt{6}$.
将边长为2的等边△OAB按如图位置放置,AB边与y轴的交点为C,则OC=$3\sqrt{2}-\sqrt{6}$.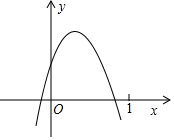 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②2a+b>0;③y随x的增大而增大;④a-b+c<0,其中正确的个数( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②2a+b>0;③y随x的增大而增大;④a-b+c<0,其中正确的个数( )