题目内容
4.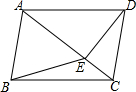 如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.(1)求证:四边形ABCD是平行四边形;
(2)若AB=BE=2,sin∠ACD=$\frac{\sqrt{3}}{2}$,求四边形ABCD的面积.
分析 (1)根据平行四边形的性质得出∠ABC+∠DCB=180°,推出∠ADC+∠BCD=180°,根据平行线的判定得出AD∥BC,根据平行四边形的判定推出即可;
(2)证明△ABE是等边三角形,得出AE=AB=2,由直角三角形的性质求出CE和DE,得出AC的长,即可求出四边形ABCD的面积.
解答 (1)证明:∵AB∥CD,
∴∠ABC+∠DCB=180°,
∵∠ABC=∠ADC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形;
(2)解:∵sin∠ACD=$\frac{\sqrt{3}}{2}$,
∴∠ACD=60°,
∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=2,
∴∠BAC=∠ACD=60°,
∵AB=BE=2,
∴△ABE是等边三角形,
∴AE=AB=2,
∵DE⊥AC,
∴∠CDE=90°-60°=30°,
∴CE=$\frac{1}{2}$CD=1,
∴DE=$\sqrt{3}$CE=$\sqrt{3}$,AC=AE+CE=3,
∴平行四边形ABCD的面积=2△ACD的面积=AC•DE=3$\sqrt{3}$.
点评 本题考查了平行四边形的性质和判定,平行线的性质和判定,等边三角形的判定与性质,含30°角的直角三角形性质的应用,能综合运用定理进行推理和计算是解此题的关键.

练习册系列答案
相关题目
15. 某物体的三视图如图,那么该物体形状可能是( )
某物体的三视图如图,那么该物体形状可能是( )
 某物体的三视图如图,那么该物体形状可能是( )
某物体的三视图如图,那么该物体形状可能是( )| A. | 长方体 | B. | 圆锥 | C. | 正方体 | D. | 圆柱 |
16.以下是某校九年级10名同学参加学校演讲比赛的统计表:则这组数据的中位数和众数分别为( )
| 成绩(分) | 80 | 85 | 90 | 95 |
| 人数(人) | 1 | 2 | 5 | 2 |
| A. | 90,89 | B. | 90,90 | C. | 90,90.5 | D. | 90,95 |
13. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 圆柱 |
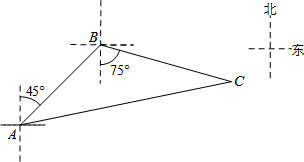 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度. 如图,货轮在海上以30海里/时的速度匀速航行,为了确定船位,当货轮在B点时,观察灯塔A在其南偏东60°方向上,货轮沿南偏东30°方向航行半小时到达C点,观察灯塔A在其北偏东75°方向上,求此时货轮距离灯塔A的距离(即AC的长)(结果保留一位小数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,货轮在海上以30海里/时的速度匀速航行,为了确定船位,当货轮在B点时,观察灯塔A在其南偏东60°方向上,货轮沿南偏东30°方向航行半小时到达C点,观察灯塔A在其北偏东75°方向上,求此时货轮距离灯塔A的距离(即AC的长)(结果保留一位小数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)