题目内容
4.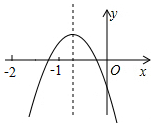 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )| A. | 4ac<b2 | B. | abc<0 | C. | b+c>3a | D. | a<b |
分析 根据二次函数的图象与性质即可求出答案.
解答 解:(A)由图象可知:△>0,
∴b2-4ac>0,
∴b2>4ac,故A正确;
∵抛物线开口向下,
∴a<0,
∵抛物线与y轴的负半轴,
∴c<0,
∵抛物线对称轴为x=-$\frac{b}{2a}$<0,
∴b<0,
∴abc<0,故B正确;
∵当x=-1时,
y=a-b+c>0,
∴a+c>b,∵b>2a
∴a+b+c>2b>4a,b+c>3a故C正确;
∵当x=-1时
y=a-b+c>0,
∴a-b+c>c,
∴a-b>0,
∴a>b,故D错误;
故选(D)
点评 本题考查二次函数图象与性质,解题的关键是熟练运用二次函数的性质,本题属于中等题型,

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
14.已知关于x的方程x2-3mx+2(m-1)=0的两根为x1、x2,且$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{3}{4}$,则m的值是多少?
19. 如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )
如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )
 如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )
如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 60° |
13.小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{9}$ |




 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限内交于点P(a,b),则a与b的数量关系是a+b=0.
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限内交于点P(a,b),则a与b的数量关系是a+b=0.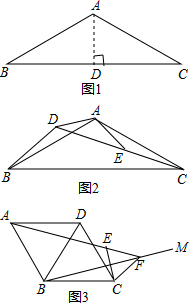 问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=$\frac{1}{2}$∠BAC=60°,于是$\frac{BC}{AB}$=$\frac{2BD}{AB}$=$\sqrt{3}$;
问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=$\frac{1}{2}$∠BAC=60°,于是$\frac{BC}{AB}$=$\frac{2BD}{AB}$=$\sqrt{3}$;