题目内容
2. 将边长为2的等边△OAB按如图位置放置,AB边与y轴的交点为C,则OC=$3\sqrt{2}-\sqrt{6}$.
将边长为2的等边△OAB按如图位置放置,AB边与y轴的交点为C,则OC=$3\sqrt{2}-\sqrt{6}$.
分析 如图,作辅助线,构建两个直角三角形,证明△ADC是30°的直角三角形,△COD是等腰直角三角形,设AD=x,则AC=2x,CD=$\sqrt{3}$x,根据OA=2列方程求出x的值,计算OC的长即可.
解答  解:如图,过C作CD⊥OA于D,
解:如图,过C作CD⊥OA于D,
∵△AOB是等边三角形,
∴∠A=60°,
Rt△ADC中,∠ACD=30°,
∴AC=2AD,
设AD=x,则AC=2x,CD=$\sqrt{3}$x,
∵∠AOE=45°,
∴∠AOC=45°,
∴△COD是等腰直角三角形,
∴OD=CD=$\sqrt{3}$x,
∴OC=$\sqrt{6}$x,
∵OA=2,
∴$\sqrt{3}$x+x=2,
x=$\sqrt{3}$-1,
∴OC=$\sqrt{6}$x=$\sqrt{6}$($\sqrt{3}$-1)=3$\sqrt{2}$-$\sqrt{6}$,
故答案为:3$\sqrt{2}$-$\sqrt{6}$.
点评 本题考查了等边三角形的性质、30°角的直角三角形的性质、等腰直角三角形的性质和判定,本题作出辅助线是关键,设一条边为未知数,将其他边分别表示出来,并找一等量关系列方程解决问题.

练习册系列答案
相关题目
13. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 圆柱 |
7.5月14日-15日“一路一带”国际合作高峰论坛在北京举行,世界的目光再次聚焦中国,某网站调查显示截至5月22日有174万余人关注此次峰会,174万用科学记数法可表示为( )
| A. | 0.174×107 | B. | 1.74×106 | C. | 1.74×105 | D. | 17.4×105 |
14.已知关于x的方程x2-3mx+2(m-1)=0的两根为x1、x2,且$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{3}{4}$,则m的值是多少?
11. 如图,AD是⊙O的直径,弦BC⊥AD,若∠AOB=50°,则∠ADC=( )
如图,AD是⊙O的直径,弦BC⊥AD,若∠AOB=50°,则∠ADC=( )
 如图,AD是⊙O的直径,弦BC⊥AD,若∠AOB=50°,则∠ADC=( )
如图,AD是⊙O的直径,弦BC⊥AD,若∠AOB=50°,则∠ADC=( )| A. | 25° | B. | 40° | C. | 50° | D. | 130° |
 如图,货轮在海上以30海里/时的速度匀速航行,为了确定船位,当货轮在B点时,观察灯塔A在其南偏东60°方向上,货轮沿南偏东30°方向航行半小时到达C点,观察灯塔A在其北偏东75°方向上,求此时货轮距离灯塔A的距离(即AC的长)(结果保留一位小数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,货轮在海上以30海里/时的速度匀速航行,为了确定船位,当货轮在B点时,观察灯塔A在其南偏东60°方向上,货轮沿南偏东30°方向航行半小时到达C点,观察灯塔A在其北偏东75°方向上,求此时货轮距离灯塔A的距离(即AC的长)(结果保留一位小数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)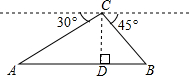 如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是200($\sqrt{3}$+1)米(结果保留根号).
如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是200($\sqrt{3}$+1)米(结果保留根号). 某学校开展了以“人生观、价值观”为主题的班会活动,活动结束后,九年级某班一小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
某学校开展了以“人生观、价值观”为主题的班会活动,活动结束后,九年级某班一小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.