Question

3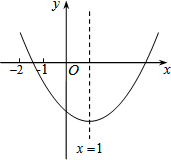．已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有下列结论：
①b²-4ac＞0；②2a-b=0；③abc＞0；④8a+c＞0；⑤9a+3b+c＜0，
其中正确结论的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

解答 解：①由图知：抛物线与x轴有两个不同的交点，则△=b²-4ac＞0，故①正确；
②抛物线的对称轴为x=-$\frac{b}{2a}$=1，则b=-2a，2a+b=0，故②错误；
③抛物线开口向上，得：a＞0；b=-2a，故b＜0；
抛物线交y轴于负半轴，得：c＜0；
所以abc＞0；故③正确；
④观察图象得当x=-2时，y＞0，
即4a-2b+c＞0，
∵b=-2a，
∴4a+4a+c＞0，即8a+c＞0，故④正确；
⑤根据抛物线的对称轴方程可知：（-1，0）关于对称轴的对称点是（3，0）；
当x=-1时，y＜0，所以当x=3时，也有y＜0，即9a+3b+c＜0；故⑤正确；
综上所述，正确的说法是：①③④⑤．
故选D．

点评 主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．