题目内容
 如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于E、D,连接CE、CD.
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于E、D,连接CE、CD.(1)求证:直线AB是圆O的切线;
(2)证明:∠BCD=∠E;
(3)证明:BC2=BD•BE.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)连接OC,根据OA=OB,CA=CB,可以证明OC⊥AB,利用切线的判定定理,经过半径的外端,并且垂直于这条半径的直线是圆的切线,得到AB是⊙O的切线;
(2)根据ED是直径,得到∠ECD=90°,从而得到∠E+∠EDC=90°,然后根据∠BCD+∠OCD=90°,∠OCD=∠ODC,得到∠BCD=∠E即可;
(3)根据前面题目的条件和∠CBD=∠EBC,证得△BCD∽△BEC,利用相似三角形的性质列出比例式求解即可.
(2)根据ED是直径,得到∠ECD=90°,从而得到∠E+∠EDC=90°,然后根据∠BCD+∠OCD=90°,∠OCD=∠ODC,得到∠BCD=∠E即可;
(3)根据前面题目的条件和∠CBD=∠EBC,证得△BCD∽△BEC,利用相似三角形的性质列出比例式求解即可.
解答: 解:(1)证明:如图,连接OC.
解:(1)证明:如图,连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB,
∴AB是圆O的切线;
(2)∵ED是直径,
∴∠ECD=90°,
∴∠E+∠EDC=90°,
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
∴∠BCD=∠E;
(3)由(2),又∵∠CBD=∠EBC,
∴△BCD∽△BEC,
∴
=
,
∴BC2=BD•BE;
 解:(1)证明:如图,连接OC.
解:(1)证明:如图,连接OC. ∵OA=OB,CA=CB,
∴OC⊥AB,
∴AB是圆O的切线;
(2)∵ED是直径,
∴∠ECD=90°,
∴∠E+∠EDC=90°,
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,
∴∠BCD=∠E;
(3)由(2),又∵∠CBD=∠EBC,
∴△BCD∽△BEC,
∴
| BC |
| BE |
| BD |
| BC |
∴BC2=BD•BE;
点评:本题考查切线的判定及性质、勾股定理、相似三角形的判定与性质等知识,包括切线的判定,线段等量关系的证明及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,?ABCD中,E在AD边上,AE=DC,F为?ABCD外一点,连接AF、BF,连接EF交AB于G,且∠EFB=∠C=60°.
如图,?ABCD中,E在AD边上,AE=DC,F为?ABCD外一点,连接AF、BF,连接EF交AB于G,且∠EFB=∠C=60°.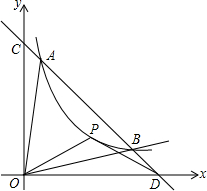 如图,直线y=-x+b(b>0)与双曲线y=
如图,直线y=-x+b(b>0)与双曲线y=