题目内容
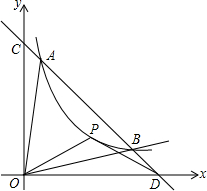 如图,直线y=-x+b(b>0)与双曲线y=
如图,直线y=-x+b(b>0)与双曲线y=| k |
| x |
(1)试用k、b表示C、D两点的坐标;
(2)若△POD得面积等于1,试求双曲线在第一象限内的分支的函数解析式;
(3)当k=1时,若△AOB得面积等于4
| 3 |
考点:反比例函数综合题
专题:综合题
分析:(1)根据坐标轴上点的坐标特征可得到C点坐标为(0,b),D点坐标为(b,0);
(2)由|PO|=|PD|得到P点的横坐标为
,则利用反比例函数图象上点的坐标特征可得到P点的坐标为(
,
),再根据三角形面积公式得S△POD=
•b•
=1,解得k=1,于是可确定反比例函数的解析式为y=
(x>0);
(3)作OM⊥CD于M,AQ⊥x轴于Q,BH⊥AQ于H,易得△OCD和△ABH都是等腰直角三角形,根据其性质得OM=
AB=
b,AB=
BH,把反比例函数解析式和一次函数解析式联立组成方程组
,消去y得到x2-bx+1=0,利用求根公式解方程,可得到点A和点B的横坐标分别为
、
,
则BH=
-
=
,所以AB=
•
,利用三角形面积公式得
•
b•
•
=4
,变形为b4-4b2-128=0,解得b1=4,b2=-4(舍去),则OC=OD=4,然后利用△COA与△BOD的面积之和=S△OCD-S△OAB进行计算.
(2)由|PO|=|PD|得到P点的横坐标为
| b |
| 2 |
| b |
| 2 |
| 2k |
| b |
| 1 |
| 2 |
| 2k |
| b |
| 1 |
| x |
(3)作OM⊥CD于M,AQ⊥x轴于Q,BH⊥AQ于H,易得△OCD和△ABH都是等腰直角三角形,根据其性质得OM=
| 1 |
| 2 |
| ||
| 2 |
| 2 |
|
b-
| ||
| 2 |
b+
| ||
| 2 |
则BH=
b+
| ||
| 2 |
b-
| ||
| 2 |
| b2-4 |
| 2 |
| b2-4 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| b2-4 |
| 3 |
解答:解:(1)把x=0代入y=-x+b得y=b;把y=0代入y=-x+b得-x+b=0,解得x=b,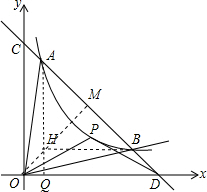
所以C点坐标为(0,b),D点坐标为(b,0);
(2)∵|PO|=|PD|,
∴P点的横坐标为
,
把x=
代入y=
得y=
=
,
∴P点的坐标为(
,
),
∴S△POD=
•b•
=1,解得k=1,
∴反比例函数的解析式为y=
(x>0);
(3)作OM⊥CD于M,AQ⊥x轴于Q,BH⊥AQ于H,
∵OC=OD=b,
∴△OCD为等腰直角三角形,
∴OM=
AB=
•
b=
b,
∵△ABH为等腰直角三角形,
∴AB=
BH,
由
得-x+b=
,
整理得x2-bx+1=0,解得x1=
,x2=
,
∴点A和点B的横坐标分别为
、
,
∴BH=
-
=
,
∴AB=
•
,
∵S△OAB=
OM•AB,
∴
•
b•
•
=4
,
变形为b4-4b2-128=0,解得b1=4,b2=-4(舍去),
∴OC=OD=4,
∴△COA与△BOD的面积之和=S△OCD-S△OAB=
×4×4-4
=8-4
.

所以C点坐标为(0,b),D点坐标为(b,0);
(2)∵|PO|=|PD|,
∴P点的横坐标为
| b |
| 2 |
把x=
| b |
| 2 |
| k |
| x |
| k | ||
|
| 2k |
| b |
∴P点的坐标为(
| b |
| 2 |
| 2k |
| b |
∴S△POD=
| 1 |
| 2 |
| 2k |
| b |
∴反比例函数的解析式为y=
| 1 |
| x |
(3)作OM⊥CD于M,AQ⊥x轴于Q,BH⊥AQ于H,
∵OC=OD=b,
∴△OCD为等腰直角三角形,
∴OM=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∵△ABH为等腰直角三角形,
∴AB=
| 2 |
由
|
| 1 |
| x |
整理得x2-bx+1=0,解得x1=
b-
| ||
| 2 |
b+
| ||
| 2 |
∴点A和点B的横坐标分别为
b-
| ||
| 2 |
b+
| ||
| 2 |
∴BH=
b+
| ||
| 2 |
b-
| ||
| 2 |
| b2-4 |
∴AB=
| 2 |
| b2-4 |
∵S△OAB=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| b2-4 |
| 3 |
变形为b4-4b2-128=0,解得b1=4,b2=-4(舍去),
∴OC=OD=4,
∴△COA与△BOD的面积之和=S△OCD-S△OAB=
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查了反比例函数的综合题:熟练掌握反比例函数图象上点的坐标特征、等腰直角三角形的性质;会求一次函数与反比例函数图象交点坐标和三角形面积.

练习册系列答案
相关题目
 如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于E、D,连接CE、CD.
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于E、D,连接CE、CD.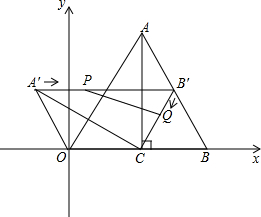 如图,在平面直角坐标系中,Rt△AOC的顶点O在坐标原点,直角顶点C在x轴的正半轴上,顶点A在第一象限.以AC为轴将△AOC翻折得到△ACB,然后将△ACB绕点C逆时针旋转60°,得到△A′CB′.已知OA=4cm,∠OAC=30°.
如图,在平面直角坐标系中,Rt△AOC的顶点O在坐标原点,直角顶点C在x轴的正半轴上,顶点A在第一象限.以AC为轴将△AOC翻折得到△ACB,然后将△ACB绕点C逆时针旋转60°,得到△A′CB′.已知OA=4cm,∠OAC=30°. 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=