题目内容
18.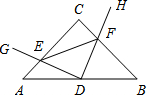 在 Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.结论:①AE+BF=$\frac{{\sqrt{2}}}{2}$AB,②AE2+BF2=EF2,③△DEF恒为等腰直角三角形,④S四边形CEDF=$\frac{1}{2}$S△ABC.其中正确的是( )
在 Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.结论:①AE+BF=$\frac{{\sqrt{2}}}{2}$AB,②AE2+BF2=EF2,③△DEF恒为等腰直角三角形,④S四边形CEDF=$\frac{1}{2}$S△ABC.其中正确的是( )| A. | ①②③④ | B. | ①②③ | C. | ①③ | D. | ②④ |
分析 连接CD,只要证明△ADE≌△CDF(ASA),即可推出AE=CF,DE=DF,S△ADE=S△CDF.由AC=BC,推出AC-AE=BC-CF,推出CE=BF,由此即可一一判断.
解答 解:连接CD,∵AC=BC,点D为AB中点,∠ACB=90°,
∴AD=CD=BD=$\frac{1}{2}$AB.∠A=∠B=∠ACD=∠BCD=45°,∠ADC=∠BDC=90°.
∴∠ADE+∠EDC=90°,
∵∠EDC+∠FDC=∠GDH=90°,
∴∠ADE=CDF.
在△ADE和△CDF中,
$\left\{\begin{array}{l}{∠A=∠DCB}\\{AD=CD}\\{∠ADE=∠CDF}\end{array}\right.$,
∴△ADE≌△CDF(ASA),
∴AE=CF,DE=DF,S△ADE=S△CDF.
∵AC=BC,
∴AC-AE=BC-CF,
∴CE=BF.
∵AC=AE+CE,
∴AC=AE+BF.
∵AC2+BC2=AB2,
∴AC=$\frac{\sqrt{2}}{2}$AB,
∴AE+BF=$\frac{\sqrt{2}}{2}$AB,故①正确,
∵DE=DF,∠GDH=90°,
∴△DEF始终为等腰直角三角形,故③
∵CE2+CF2=EF2,
∴AE2+BF2=EF2故②正确,
∵S四边形CEDF=S△EDC+S△EDF,
∴S四边形CEDF=S△EDC+S△ADE=$\frac{1}{2}$S△ABC.故④正确.
∴正确的有①②③④.
故选A.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定及性质、勾股定理、三角形的面积等知识,解题的关键是证明△ADE≌△CDF,属于中考常考题型.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
8. 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,若矩形的面积是6,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,若矩形的面积是6,则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,若矩形的面积是6,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,若矩形的面积是6,则k的值为( )| A. | -6 | B. | -5 | C. | 6 | D. | 5 |
13.如图是某一计算程序,例如:当输入x=150时,输出结果是301;当输入x=100时,输出结果是403;若输入x的值是正整数,输出结果是407,则满足条件的x的值最多有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.如果$\sqrt{2a+{b}^{2}}$+|b2-10|=0,那么a,b的值分别为( )
| A. | 5,$\sqrt{10}$ | B. | -5,$\sqrt{10}$ | C. | 5,±$\sqrt{10}$ | D. | -5,±$\sqrt{10}$ |
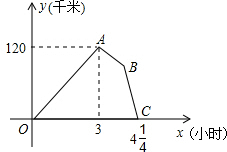 快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地后停留了45分钟,立即按原路以另一速度匀速返回,直至与慢车相遇.已知慢车的速度为60千米/时,两车之间的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,则快车从乙地返回时的速度为90千米/时.
快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地后停留了45分钟,立即按原路以另一速度匀速返回,直至与慢车相遇.已知慢车的速度为60千米/时,两车之间的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,则快车从乙地返回时的速度为90千米/时.