题目内容
9.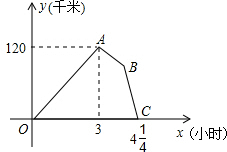 快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地后停留了45分钟,立即按原路以另一速度匀速返回,直至与慢车相遇.已知慢车的速度为60千米/时,两车之间的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,则快车从乙地返回时的速度为90千米/时.
快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地后停留了45分钟,立即按原路以另一速度匀速返回,直至与慢车相遇.已知慢车的速度为60千米/时,两车之间的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,则快车从乙地返回时的速度为90千米/时.
分析 设快车从甲地到乙地的速度为x千米/时,根据3小时相距120千米即可列方程求解,根据条件AB段所用的时间是45分钟,利用甲和乙之间的距离减去慢车行驶的距离即可求得B点对应的横坐标,设快车从乙地返回甲地的速度是y千米/小时,根据距离公式即可列方程求解.
解答 解:设快车从甲地到乙地的速度为x千米/时,则
3(x-60)=120,
x=100.
则甲、乙两地之间的距离是3×100=300(千米);
快车返回时距离慢车的距离是:300-60(3+$\frac{45}{60}$)=75(千米),
设快车从乙地返回甲地的速度是y千米/小时.
根据题意得:(60+y)[4 $\frac{1}{4}$-(3+$\frac{45}{60}$)]=75,
解得:y=90.
则快车从乙地返回甲地的速度是90千米/小时.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题,关键是根据一次函数的性质和图象结合实际问题求解.

练习册系列答案
相关题目
19.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程kx+3y=1的一个解,那么k的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
17.下列图形既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.下列图形中既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

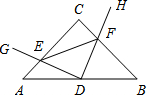 在 Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.结论:①AE+BF=$\frac{{\sqrt{2}}}{2}$AB,②AE2+BF2=EF2,③△DEF恒为等腰直角三角形,④S四边形CEDF=$\frac{1}{2}$S△ABC.其中正确的是( )
在 Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG,DH分别与边AC,BC交于E,F两点.结论:①AE+BF=$\frac{{\sqrt{2}}}{2}$AB,②AE2+BF2=EF2,③△DEF恒为等腰直角三角形,④S四边形CEDF=$\frac{1}{2}$S△ABC.其中正确的是( )