题目内容
2.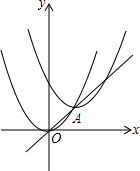 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )| A. | y=(x+2)2-2 | B. | y=(x+2)2+2 | C. | y=(x-2)2+2 | D. | y=(x-2)2-2 |
分析 首先根据A点所在位置设出A点坐标为(m,m),再根据AO=2$\sqrt{2}$,利用勾股定理求出m的值,然后根据抛物线平移的性质:左加右减,上加下减可得解析式.
解答 解:∵A在直线y=x上,
∴设A(m,m),
∵OA=2$\sqrt{2}$,
∴m2+m2=(2$\sqrt{2}$)2,
解得:m=±2(m=-2舍去),
∴m=2,
∴A(2,2),
∴抛物线解析式为:y=(x-2)2+2,
故选:C.
点评 此题主要考查了二次函数图象的几何变换,关键是求出A点坐标,掌握抛物线平移的性质:左加右减,上加下减.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
13. 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )
 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
7.下列命题中,是真命题的是( )
| A. | 相等的角是对顶角 | B. | 垂线段最短 | ||
| C. | $\sqrt{81}$的平方根是±9 | D. | 无限小数都是无理数 |
14. 已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
 已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )| A. | △ADC∽△ACB | B. | △BDC∽△BCA | C. | △ADC∽△CBD | D. | 无法判断 |
12. 如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )
 如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,
如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,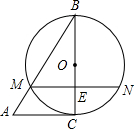 如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=$\sqrt{3}$.
如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=$\sqrt{3}$.