题目内容
17.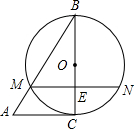 如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=$\sqrt{3}$.
如图,在△ABC中,以BC为直径的⊙O交AB于M,弦MN∥AC且MN交BC于点E,ME=1,BM=2,BE=$\sqrt{3}$.(1)求证AC是⊙O的切线;
(2)求弧NC的长度.
分析 (1)根据勾股定理的逆定理证明∠BEM=90°,根据平行线的性质得到∠ACB=90°,根据切线的判定定理证明;
(2)根据正弦的定义和垂径定理求出∠CON=60°,利用弧长公式计算即可.
解答 (1)证明:∵ME=1,BM=2,BE=$\sqrt{3}$,
∴ME2+BE2=1+3=4,BM2=4,
∴ME2+BE2=BM2,
∴∠BEM=90°,又MN∥AC,
∴∠ACB=∠BEM=90°,
∴AC是⊙O的切线;
(2)连接ON,
∵∠BEM=90°,ME=1,BM=2,
∴∠B=30°,$\widehat{MC}$=$\widehat{NC}$,NE=ME=1,
∴∠CON=60°,
ON=$\frac{EN}{sin∠CON}$=$\frac{2\sqrt{3}}{3}$,
故弧NC的长度为:$\frac{60×π×\frac{2\sqrt{3}}{3}}{180}$=$\frac{2\sqrt{3}π}{9}$.
点评 本题考查的是切线的判定、垂径定理、弧长的计算、勾股定理的逆定理,掌握经过半径的外端且垂直于这条半径的直线是圆的切线、弧长公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R)是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
8.一种甲型H1N1流感病毒的直径约为0.00000078m,数0.00000078用科学记数法表示为( )
| A. | 0.78×10-5 | B. | 7.8×10-6 | C. | 7.8×10-7 | D. | 78×10-8 |
5.关于x的方程x2-4x+4a=0有两个实数根,则a的取值范围是( )
| A. | a<1 | B. | a>1 | C. | a≤1 | D. | a≥1 |
2.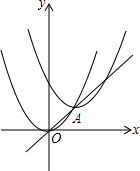 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )| A. | y=(x+2)2-2 | B. | y=(x+2)2+2 | C. | y=(x-2)2+2 | D. | y=(x-2)2-2 |