题目内容
11.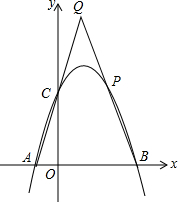 抛物线y=-x2+2x+3交x轴于点A,B,交y轴于点C,点P为抛物线第一象限内的点,直线BP交直线AC于点Q,若点P为BQ的中点,求点P的坐标.
抛物线y=-x2+2x+3交x轴于点A,B,交y轴于点C,点P为抛物线第一象限内的点,直线BP交直线AC于点Q,若点P为BQ的中点,求点P的坐标.
分析 由抛物线的解析式求出A(-1,0),B(3,0),C(0,3),利用待定系数法求出直线AC的解析式为y=3x+3,由直线AC过点Q,可设Q点的坐标为(x,3x+3),再根据点P为BQ的中点,利用中点坐标公式得出P($\frac{x+3}{2}$,$\frac{3x+3}{2}$),然后将P点坐标代入y=-x2+2x+3,求出x的值,进而求出点P的坐标.
解答 解:∵y=-x2+2x+3,
∴y=0时,-x2+2x+3=0,
解得x=-1或3,
∴A(-1,0),B(3,0),
∵x=0时,y=3,
∴C(0,3).
设直线AC的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-k+b=0}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$,
∴直线AC的解析式为y=3x+3,
∴可设Q点的坐标为(x,3x+3).
∵点P为BQ的中点,B(3,0),
∴P($\frac{x+3}{2}$,$\frac{3x+3}{2}$).
∵点P为抛物线y=-x2+2x+3第一象限内的点,
∴$\frac{3x+3}{2}$=-($\frac{x+3}{2}$)2+2×($\frac{x+3}{2}$)+3,
整理,得x2+8x-9=0,
解得x1=1,x2=-9(不合题意舍去),
当x=1时,点P的坐标是(2,3).
点评 本题考查了抛物线与x轴的交点,二次函数图象上点的坐标特征,待定系数法求直线的解析式,线段中点坐标公式等知识,综合性较强,难度适中.设Q点的坐标为(x,3x+3),用含x的代数式表示出P点坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知点A(4,y1),B($\sqrt{2}$,y2),C(-2,y3)都在y=$\frac{9}{x}$上,试判断y1,y2,y3的大小关系( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y1<y3<y2 |
 完成下面的证明.
完成下面的证明.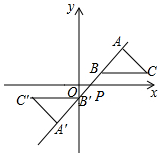 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为(-2,-3).
如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为(-2,-3).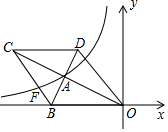 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上反比例函数y=$\frac{k}{x}({x<0})$的图象经过菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(-6,8),则k的值为-32.
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上反比例函数y=$\frac{k}{x}({x<0})$的图象经过菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(-6,8),则k的值为-32. 如图,△ABC与△DCB中,AC与BD交于点O,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点O,且∠A=∠D,AB=DC. 如图,在?ABCD中,点E在DA的延长线上,点F在BC的延长线上,且BE∥FD.求证:∠ABE=∠CDF.
如图,在?ABCD中,点E在DA的延长线上,点F在BC的延长线上,且BE∥FD.求证:∠ABE=∠CDF.