题目内容
14. 完成下面的证明.
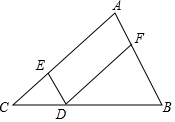
完成下面的证明.如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,且∠FDE=∠A,求证:DF∥CA.
证明:∵DE∥BA,
∴∠A=∠CED(两直线平行,同位角相等)
∵∠FDE=∠A
∴∠FDE=∠CED(等量代换)
∴DF∥CA(内错角相等,两直线平行)
分析 根据平行线的性质,得到∠A=∠CED,再根据平行线的判定,即可得出DF∥CA.
解答 证明:∵DE∥BA,
∴∠A=∠CED( 两直线平行,同位角相等)
∵∠FDE=∠A
∴∠FDE=∠CED (等量代换)
∴DF∥CA(内错角相等,两直线平行)
故答案为:∠CED,两直线平行,同位角相等;∠CED,等量代换;内错角相等,两直线平行.
点评 本题主要考查了平行线的性质与判定的运用,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
2. 如图,AB∥CD,∠A=70°,则∠1的度数是( )
如图,AB∥CD,∠A=70°,则∠1的度数是( )
 如图,AB∥CD,∠A=70°,则∠1的度数是( )
如图,AB∥CD,∠A=70°,则∠1的度数是( )| A. | 130° | B. | 110° | C. | 100° | D. | 70° |
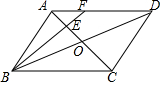 如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
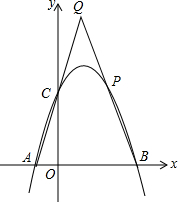 抛物线y=-x2+2x+3交x轴于点A,B,交y轴于点C,点P为抛物线第一象限内的点,直线BP交直线AC于点Q,若点P为BQ的中点,求点P的坐标.
抛物线y=-x2+2x+3交x轴于点A,B,交y轴于点C,点P为抛物线第一象限内的点,直线BP交直线AC于点Q,若点P为BQ的中点,求点P的坐标. 已知,如图,AB∥CD,∠1=∠2,那么∠E和∠F相等吗?为什么?
已知,如图,AB∥CD,∠1=∠2,那么∠E和∠F相等吗?为什么?