题目内容
14.若扇形的半径为3,扇形的面积为2π,则该扇形的圆心角为80度.分析 首先设该扇形的圆心角度数为n°,由扇形的面积为2π,半径为3,利用扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=$\frac{nπ{R}^{2}}{360}$,即可得方程:2π=$\frac{nπ×{3}^{2}}{360}$,解此方程即可求得答案.
解答 解:设该扇形的圆心角度数为n°,
∵扇形的面积为2π,半径为3,
∴2π=$\frac{nπ×{3}^{2}}{360}$,
解得:n=80.
∴该扇形的圆心角度数为80°.
故答案为:80.
点评 此题考查了扇形面积的计算.此题比较简单,注意熟记公式与性质是解此题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
2.已知x=$\sqrt{2}$+1,y=$\sqrt{2}$-1,则x2-5xy+y2+6等于( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
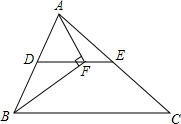 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为3.
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为3. 甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图11所示,乙在A处提速后的速度是甲登山速度的3.根据图象所提供的信息解答下列问题中正确的个数为( )
甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图11所示,乙在A处提速后的速度是甲登山速度的3.根据图象所提供的信息解答下列问题中正确的个数为( )