题目内容
3. 甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图11所示,乙在A处提速后的速度是甲登山速度的3.根据图象所提供的信息解答下列问题中正确的个数为( )
甲乙两人同时登西山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图11所示,乙在A处提速后的速度是甲登山速度的3.根据图象所提供的信息解答下列问题中正确的个数为( )(1)甲登山的速度是每分钟10 米.
(2)乙在A地提速时距地面的高度b为30 米.
(3)登山9分钟时,乙追上了甲.
(4)乙在距地面的高度为165米时追上甲.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据速度=高度÷时间即可算出甲登山上升的速度;根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;
根据函数图象和题意可以得到甲、乙二人登山全过程中,登山时距地面的高度y(米)与登山时间x(分)之间的函数关系式;根据函数图象和题意可以得到登山多长时间时,乙追上了甲.乙在距地面的高度为165米时追上甲.
解答 解:(1)(300-100)÷20=10(米/分钟),故正确;
(2)b=15÷1×2=30,故正确;
(3)当2≤x≤11时,
∵甲对应的函数关系式为:y=10x+100(0≤x≤20),乙对应的函数解析式为y=30x-30,
∴10x+100=30x-30,
解得,x=6.5
即登山6.5分钟时,乙追上了甲,故错误;
(4)将x=6.5代入y=30x-30,得y=165,
即乙在距地面的高度为165米时追上甲,故正确;
故选C.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
12.若函数y=mx2+(m-1)x+$\frac{1}{2}$(m-1)的图象与x轴只有一个交点,那么m的值是( )
| A. | 0 | B. | 0,-1或1 | C. | 1或-1 | D. | 0或1 |
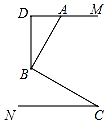 如图,已知AM∥CN,点B为平面内一点,AB⊥BC于B.过点B作BD⊥AM于点D,则图中∠ABD和∠C的关系是∠ABD=∠C.
如图,已知AM∥CN,点B为平面内一点,AB⊥BC于B.过点B作BD⊥AM于点D,则图中∠ABD和∠C的关系是∠ABD=∠C.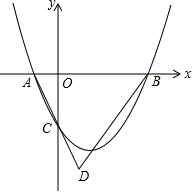 如图,抛物线y=$\frac{1}{2}{x^2}$+bx-2与x轴交于A(x1,0)、B(x2,0)两点,与y轴交于点C.
如图,抛物线y=$\frac{1}{2}{x^2}$+bx-2与x轴交于A(x1,0)、B(x2,0)两点,与y轴交于点C.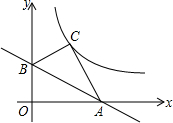 如图,已知点A(6,0),B(0,2$\sqrt{3}$),O为坐标原点,点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$(k>0)的图象上,求k的值.
如图,已知点A(6,0),B(0,2$\sqrt{3}$),O为坐标原点,点O关于直线AB的对称点C恰好落在反比例函数y=$\frac{k}{x}$(k>0)的图象上,求k的值.