题目内容
9.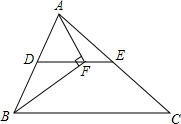 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为3.
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为3.
分析 根据直角三角形斜边上中线是斜边的一半可得DF=$\frac{1}{2}$AB=AD=BD=5且∠ABF=∠BFD,结合角平分线可得∠CBF=∠DFB,即DE∥BC,进而可得DE=8,由EF=DE-DF可得答案.
解答 解:∵AF⊥BF,
∴∠AFB=90°,
∵AB=10,D为AB中点,
∴DF=$\frac{1}{2}$AB=AD=BD=5,
∴∠ABF=∠BFD,
又∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠CBF=∠DFB,
∴DE∥BC,
∴AE=EC,
∴DE=$\frac{1}{2}$BC=8,
∴EF=DE-DF=3,
点评 本题主要考查直角三角形斜边中线的性质、三角形中位线的性质、平行线的判定和性质等知识,解题的关键是证明DE是△ABC的中位线,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16. 如图,AB∥CD,CE平分∠ACD,若∠1=25°,那么∠2的度数是( )
如图,AB∥CD,CE平分∠ACD,若∠1=25°,那么∠2的度数是( )
 如图,AB∥CD,CE平分∠ACD,若∠1=25°,那么∠2的度数是( )
如图,AB∥CD,CE平分∠ACD,若∠1=25°,那么∠2的度数是( )| A. | 160° | B. | 50° | C. | 70° | D. | 60° |
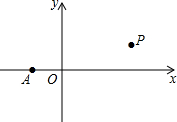 如图,在平面直角坐标系第一象限有一点P,其横坐标为3,在x轴上有一点A(-1,0),已知PA两点间的距离为2$\sqrt{5}$,则P的纵坐标为2.
如图,在平面直角坐标系第一象限有一点P,其横坐标为3,在x轴上有一点A(-1,0),已知PA两点间的距离为2$\sqrt{5}$,则P的纵坐标为2.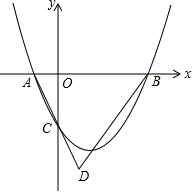 如图,抛物线y=$\frac{1}{2}{x^2}$+bx-2与x轴交于A(x1,0)、B(x2,0)两点,与y轴交于点C.
如图,抛物线y=$\frac{1}{2}{x^2}$+bx-2与x轴交于A(x1,0)、B(x2,0)两点,与y轴交于点C.