题目内容
8.已知:如图,在等边三角形ABC中,点D、E分别在直线AB、直线AC上,且AE=BD.(1)当点D、E分别在边AC、边AB上时,如图1所示,EB与CD相交于点G,求∠CGE的度数;
(2)当点D、E分别在边CA、边AB的延长线上时,如图2所示,∠CGE的度数是否变化?如不变,请说明理由.如变化,请求出∠CGE的度数.

分析 (1)根据等边三角形的性质得到AB=BC,∠A=∠ABC=60°,推出△ABE≌△BCD,根据全等三角形的性质得到∠ABE=∠BCD,根据三角形外角的性质即可得到结论;
(2)由三角形ABC为等边三角形,利用等边三角形的性质得到AB=BC,∠ACB=∠ABC=60°,利用等角的补角相等得到夹角相等,利用SAS得到三角形ABE与三角形BCD全等,利用全等三角形的对应角相等得到∠D=∠E,利用外角性质及等量代换即可得证.
解答 解:(1)证明:∵△ABC为等边三角形,
∴AB=BC,∠A=∠ABC=60°,
在△ABE和△BCD中,$\left\{\begin{array}{l}{AE=BD}\\{∠A=∠DBC}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCD,
∴∠ABE=∠BCD,
∵∠ABE+∠CBG=60°,
∴∠BDG+∠CBG=60°,
∵∠CGE=∠BCG+∠CBG,
∴∠CGE=60°;
(2)证明:∵△ABC为等边三角形,
∴AB=BC,∠CAB=∠ABC=60°,
∴∠EAB=∠CBD=120°,
在△ABE和△BCD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠EAB=∠CBD}\\{AE=BD}\end{array}\right.$,
∴△ABE≌△BCD(SAS),
∴∠D=∠E,
∵∠ABE=∠DBG,∠CAB=∠E+ABE=60°,
∴∠CGE=∠D+∠DBG=60°.
点评 此题考查了全等三角形的判定与性质,等边三角形的性质,三角形外角的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
9. 如图,在△ABC中,AB=AC,点D在边BC上,且AD⊥AC,BD=4,∠B=30°,则CD=( )
如图,在△ABC中,AB=AC,点D在边BC上,且AD⊥AC,BD=4,∠B=30°,则CD=( )
 如图,在△ABC中,AB=AC,点D在边BC上,且AD⊥AC,BD=4,∠B=30°,则CD=( )
如图,在△ABC中,AB=AC,点D在边BC上,且AD⊥AC,BD=4,∠B=30°,则CD=( )| A. | 4$\sqrt{3}$ | B. | 8 | C. | 6 | D. | 4$\sqrt{2}$ |
 、
、 与直线
与直线 相交,给出下列条件:
相交,给出下列条件:
 如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式:
如图,用四个完全一样的长、宽分别为x、y的长方形纸片围成一个大正方形ABCD,中间是空的小正方形EFGH.若AB=a,EF=b,判断以下关系式: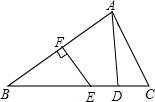 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC. 如图,在△ABC中,∠ABC=45°,H是高AD和高BE的交点,则BH和AC的大小关系如何?并说明理由.猜想:若∠ABC=135°,其他条件不变,则BH和AC的大小关系将发生什么变化?
如图,在△ABC中,∠ABC=45°,H是高AD和高BE的交点,则BH和AC的大小关系如何?并说明理由.猜想:若∠ABC=135°,其他条件不变,则BH和AC的大小关系将发生什么变化? 如图所示:
如图所示: